1 引 言
随着地下工程建造规模越来越大,地下空间的结构形式也越来越复杂,不可避免地出现隧道交叉的情况。隧道交叉段是一个空间问题,由于开挖顺序和工法的不同,在多次扰动下,围岩及其支护结构力学行为受应力重分布影响发生复杂变化,可能引起围岩的过度变形,进而导致地面建筑物和地下构筑物的开裂与破损,严重威胁隧道安全。
针对隧道交叉段稳定性问题已有大量研究,例如Hsiao等采用数值计算方法分析了不同岩石强度、交叉角度等因素对隧道稳定性的影响,并建立了评价交叉角度对隧道行为影响的标准。唐锐等使用FLAC3D软件分析了公路、铁路隧道交叉口段施工时序对隧道结构安全性的影响,并给出了交叉口段公路、铁路隧道施工顺序以便参考。赵光等利用MSC.Marc有限元软件分析了多层交叉隧道结构体系抗震性能。高广运等采用FLAC3D软件分析了某大跨巷道交叉口围岩开挖后的位移、应力及塑性区分布特征,以及影响巷道交叉段稳定性的主要因素。林达明等结合ANSYS与FLAC3D软件模拟分析了Y型隧道中单线隧道合并为双线隧道过程中应力与应变的变化规律,明确了Y型隧道设计、建设过程中的重点。Chortis等研究了施工过程中交叉段支护结构的受力特征,确定了交叉段施工影响的范围。张勇采用Midas GTS软件对地铁车站与市政隧道交叉共板合建结构进行三维有限元受力分析,明确了结构在土压力、水浮力、恒荷载和活荷载等组合载荷作用下的位移、弯矩特征及墙、板等结构应力的分布状况。朱正国等研究了隧道爆破施工对立体交叉隧道动力响应规律,确定了安全振速标准及不同影响程度的安全范围。贾宝新等研究了新建隧道不同覆土厚度、交叉角度对上部既有隧道的影响,并采用交叉间距折减的方法验证方案的安全性。徐慧芬等采用有限元法对公路与铁路立体交叉隧道施工过程进行三维数值模拟分析,结果表明爆破振动对已建铁路隧道影响较小。可以发现,上述研究多是通过不同的数值计算方法对不同形式的交叉段隧道围岩或支护结构的受力进行分析,所依托的背景工程交叉段也多为两隧道直接贯通的连接方式。
地铁暗挖车站风道进入隧道主体的施工方法主要包括门形进洞法与拱形进洞法。常规交叉隧道施工主要采用门形进洞法,形成的洞型为单向拱,而采用拱形进洞法的应用较少。在受力分析方面,已有的研究主要围绕交叉段围岩位移、应力特征及塑性区特征进行研究,对拱形进洞法形成的受力更为复杂的穹拱形空间受力规律及施工过程力学演化机制的研究较少。因此本文以某地铁暗挖车站风道与主体隧道的交叉段为例,通过数值计算与模型试验,研究对比门形进洞法与拱形进洞法下交叉段结构的受力特点,揭示风道-主体隧道交叉段等关键部位的受力转换机制,并对施工工法进行优化,保证交叉穹拱形地下空间的稳定。
2 工程概况
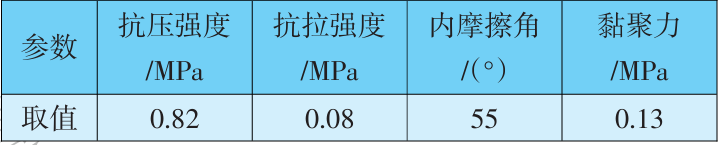
某地铁车站全长247.8m,共设置3个出入口,2组风亭和1个安全出口,其中风井兼作施工竖井,风道兼作施工通道。选取2号风道转主体隧道交叉段为研究对象,如图1所示。风道跨度为14.6m,主体隧道跨度为20.0m,埋深20.0m。场区地质从上至下依次为素填土、强风化花岗岩、中风化花岗岩和微风化花岗岩,隧道洞身主要穿过微风化花岗岩,通过对现场围岩进行取样,在实验室进行力学试验测得岩体力学相关参数,见表1,地下水类型为基岩裂隙水。
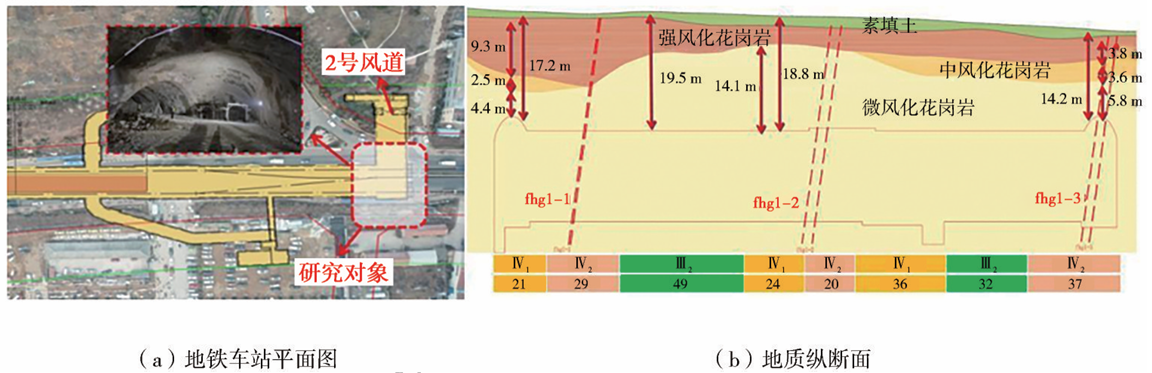
图1 地铁车站平面图及地质纵断面示意
表1 围岩物理力学参数
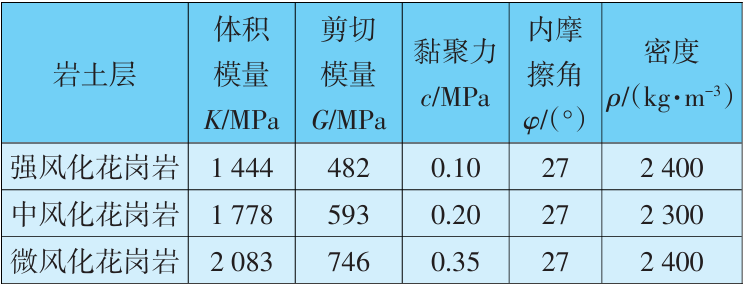
风道-主体隧道交叉段采用门形进洞法施工时,在交叉段沿某一隧道方向形成拱形,沿另一隧道方向是平面,形成的洞型称为单向拱,如图2(a)所示;采用拱形进洞法施工时,在隧道两个方向都是拱形,形成的洞型称为穹拱形(双向拱),如图2(b)所示。本文车站风道转主体隧道段选用拱形进洞法施工。
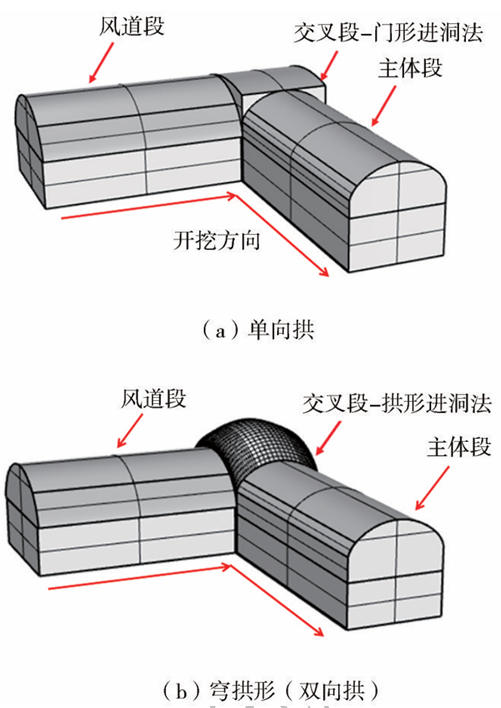
图2 单向拱和双向拱示意
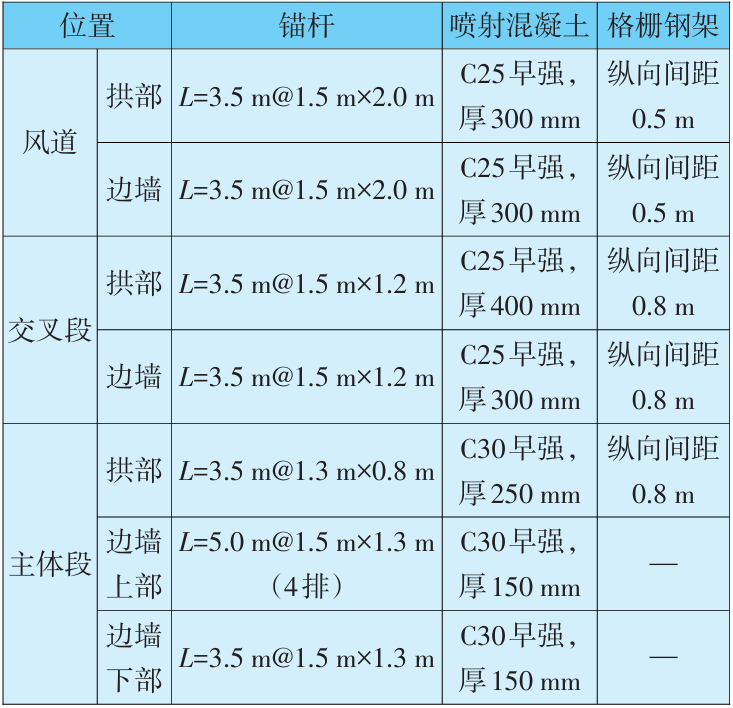
交叉段进洞按设计要求,渐变高度由横通道逐榀挑高进车站主体隧道,每榀格栅钢架进尺为0.8~1.2 m,每榀格栅钢架挑高渐变高度为0.1~1.38m,开挖完成后交叉段形成一穹拱形地下空间。风道、交叉段及主体隧道均采用复合式衬砌,初期支护采用锚杆+喷射混凝土+格栅钢架支护。交叉段拱部支护参数为:锚杆长3.5m,间距1.5m,排距1.2m;喷射C25早强混凝土,厚400mm;格栅钢架纵向间距0.8 m。交叉段边墙支护参数为:锚杆长3.5m,间距1.5 m,排距1.2 m;喷射C25早强混凝土,厚度为300 mm;格栅钢架纵向间距0.8m。
3 研究方法
本文结合数值计算和模型试验两种方法,通过数值计算对比了两种施工方式下围岩的稳定性,分析了拱形进洞施工形成的交叉穹拱形地下空间的受力特点。通过模型试验模拟交叉隧道实际开挖过程,对数值计算结果进行了验证。
3.1 数值计算
针对两种施工方式进行对比的数值计算模型未考虑隧道支护,仅模拟开挖过程;而针对拱形进洞的精细化数值计算模型则考虑了隧道支护。数值计算模型如图3所示,根据现场2号风道转主体段实际情况,考虑边界效应,模型尺寸为风道开挖方向100m,隧道开挖方向78.6m,高度为68m。使用四面体单元模拟岩体,共有124264个单元和46296个节点。计算模型的前后左右边界限制法向位移,下边界限制所有方向位移,上边界不限制位移。模型的围岩使用M-C本构模型,参数见表1。
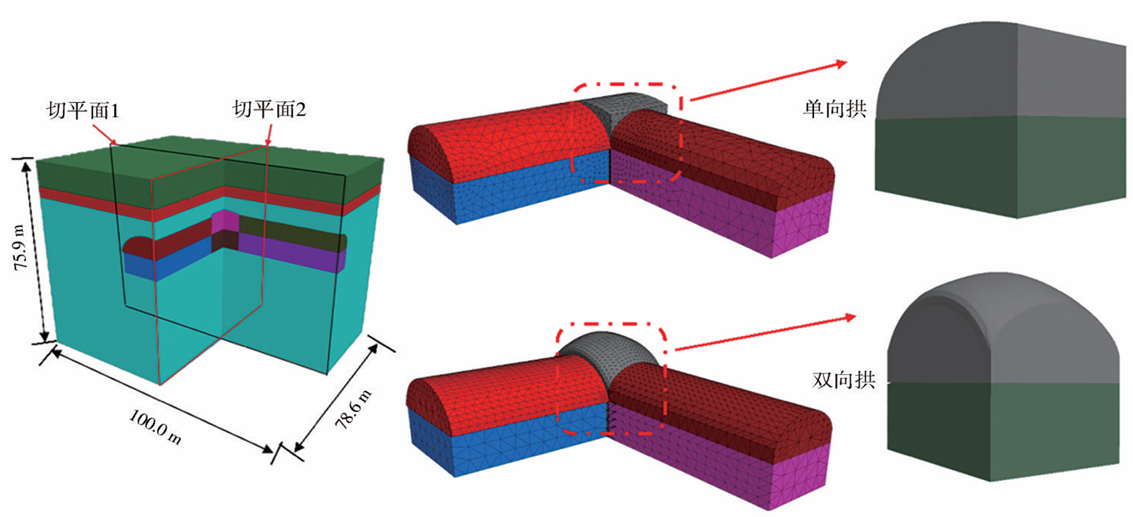
图3 两种施工方式的拱形对比数值模型
主要采用FLAC3D数值模拟软件进行分析,预应力锚杆使用Cable单元模拟,格栅钢架使用Beam单元模拟,通过命令流找到自由段和锚固段的范围,将预应力锚杆划分为托盘、自由段和锚固段。对预应力锚杆的3个部分的锚固剂赋值不同参数(锚固剂刚度、黏结力、内摩擦角)模拟实际应用状况。在地应力平衡后进行位移清零,数值模拟得到的数据主要是开挖扰动引起的。
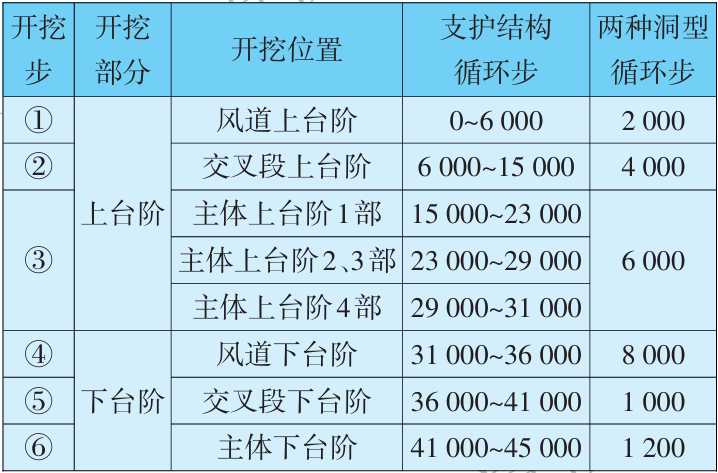
模拟的开挖顺序和现场相同,分为步序①—步序⑥,按顺序开挖。步序①—步序③分别对应风道、交叉段、主体隧道的上台阶,步序④—步序⑥分别对应风道、交叉段、主体隧道的下台阶,数值模拟循环步和开挖位置对照见表2,其中在实际工程现场,开挖与支护施工时,围岩尚未达到平衡就进入了下一阶段的循环,因此在数值模拟中,通过循环步与现场开挖支护时间进行对应,根据现场实际施工时间,确定循环步长,以求能够得到更贴近现场实际状况的数值模拟结果。
表2 数值模拟循环步与开挖步对照
支护结构系统数值计算模型如图4所示,支护结构单元参数见表3,初期支护参数见表4。其中对于锚杆支护,按照现场实际情况设置,风道段采用中空注浆锚杆支护,交叉段和主体段采用100kN的预应力锚杆支护。钢架支护与现场一致,风道和交叉段在拱部和边墙部分均架设格栅钢架,而在主体部分只在拱部架设格栅钢架。
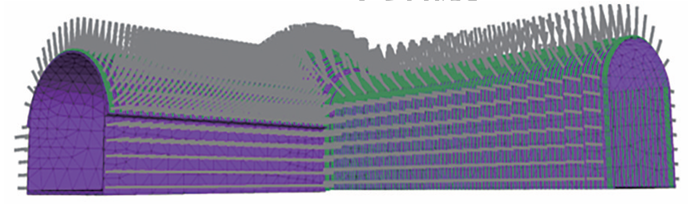
图4 考虑支护系统的数值计算模型
表3 支护结构单元参数
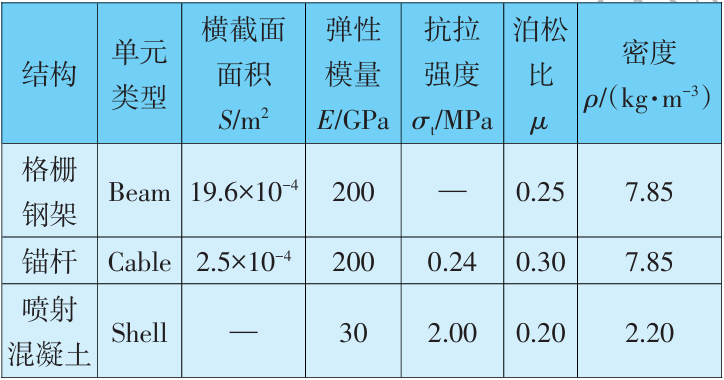
表4 初期支护参数
数值模型的开挖采用空模型,喷层、拱架、锚杆采用结构单元的形式实现。
3.2 模型试验
综合考虑岩石力学参数与试验装置尺寸,根据相似原理,试验几何相似比取80,容重相似比取1。计算得到隧道模型体长度和宽度均为1m,风道与主体隧道跨度分别为0.18m、0.25m,隧道埋深根据相似比计算设置为0.25m,顶部及边墙部分并未进行其他应力加载。以单轴抗压强度和抗拉强度为控制指标,对不同的石膏掺量进行了多组单轴压缩及巴西劈裂试验,确定配合比为石膏∶黄土∶细沙∶水=0.8∶ 4∶8∶0.5,相似材料强度参数见表5。
表5 相似材料力学参数
模型采用相似材料进行填充,分层填充夯实,确保模型内部不会形成空洞,避免对强度产生明显的影响。为实现交叉隧道分步开挖,隧道边墙部分通过相似材料填筑的方式制作并对模型体填充砌筑,隧道拱部则使用3D打印的预制体代替,如图5所示。风道段按照开挖进尺预制成小块,开挖时取出对应块即可;交叉段为与现场等比例的穹拱形状,开挖时直接取出;主体段打印左右两块预制体,开挖主体段拱部时通过抽拉预制体实现分步开挖。试验时按照风道—交叉段—主体段的顺序开挖隧道拱部(上台阶),完成后静置一段时间,使围岩变形和应力充分变化,监测数据趋于稳定后再开挖隧道边墙部分(下台阶)。

图5 隧道模型体制作及布置
模型试验对多个断面围岩的应力、应变进行监测。为收集风道-主体交叉段完整的隧道围岩力学演化规律,将测点布置在风道、交叉段和主体段多个断面的拱顶、拱腰及边墙等位置,如图6所示,通过设置应变砖对测点处的应力、应变进行监测。
图6 围岩应变监测断面及测点布置示意
4 毛洞条件下两类洞型对比分析
4.1数值模拟结果对比
(1)不同进洞方式位移对比
两种交叉段拱形的竖向位移云图如图7、图8所示。由图7可见,切平面1中单向拱最大沉降位于交叉段中部,穹拱形最大沉降位于交叉段偏向风道一侧,单向拱围岩沉降量最大值为8.0mm;由图8可见,切平面2中单向拱最大沉降位于交叉段与主体段交界处,穹拱形最大沉降位置相对更偏向主体段,单向拱与穹拱形围岩沉降量最大值均为9.0mm。
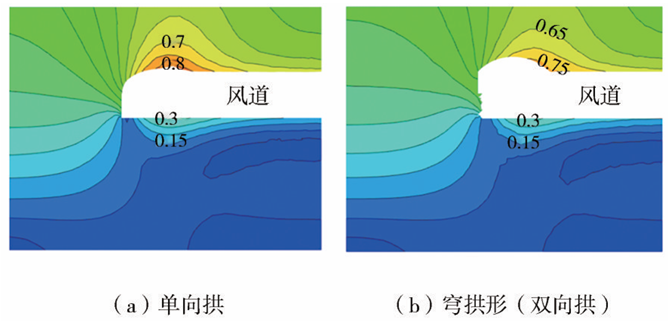
图7 不同进洞方式切平面1的沉降云图(单位:cm)
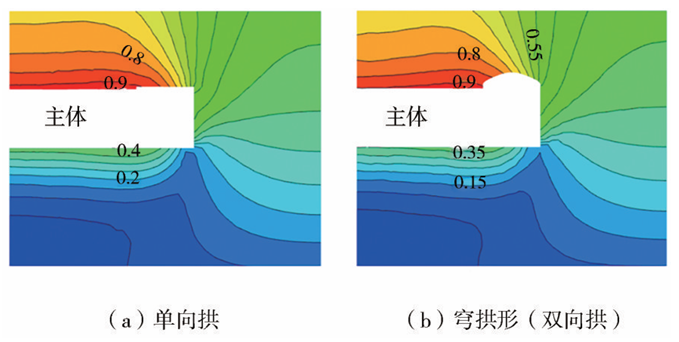
图8 不同进洞方式切平面2的沉降云图(单位:cm)
总体上,穹拱形围岩沉降较单向拱围岩沉降减少量约占总沉降量的7%,故拱形进洞法对围岩的扰动范围更小,更有利于隧道围岩的稳定。
(2)不同进洞方式围岩应力对比
在交叉段拱部布置了A、B、C3个测点,边墙布置了1个D测点,位置如图9所示。监测断面各测点围岩主应力随隧道各步开挖过程变化曲线如图10所示。
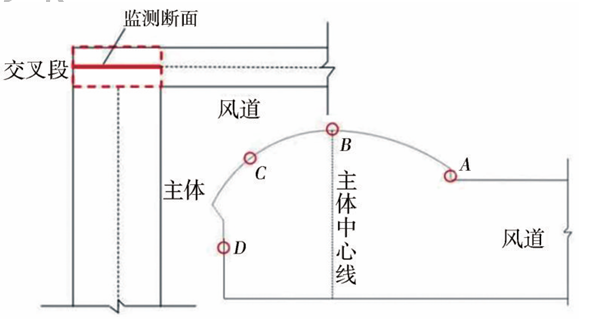
图9 监测断面位置及监测点布置
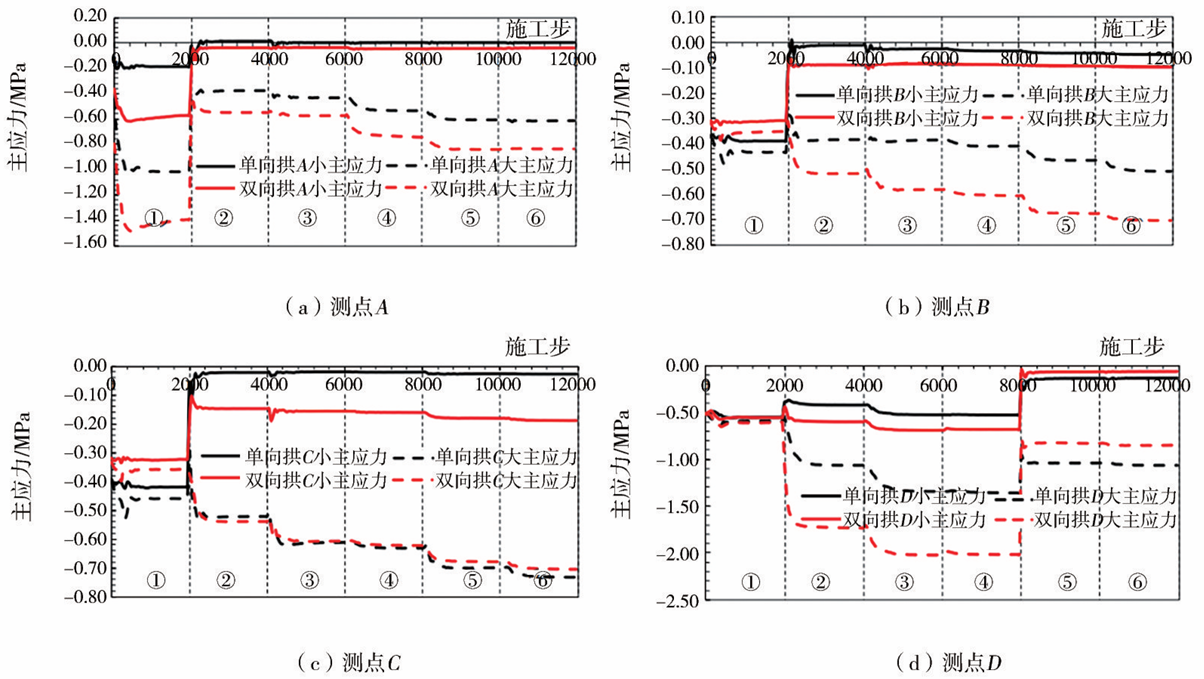
图10 监测断面各测点围岩主应力随各开挖步变化曲线
由图10可知,随着上台阶开挖逐步靠近监测断面,围岩荷载重分布使得测点B、C大主应力明显增加。由于测点A位于风道和交叉段接口处,与测点B、C的变化规律不同,测点A的大主应力减小,上台阶开挖至监测断面时,门形进洞法大、小主应力分别达到最大值-1.01MPa和-0.19MPa,拱形进洞法大、小主应力分别达到最大值-1.41MPa和-0.60MPa;监测断面开挖后,荷载瞬间释放,门形进洞法测点A大、小主应力减少至-0.38MPa和-0.01MPa,拱形进洞法测点A大、小主应力减至-0.54MPa和-0.04MPa;经过断面继续向前推进,大、小主应力缓慢增加,大约增加至最大值的一半。对交叉段拱顶测点B展开分析,两种施工方法下随着开挖步序的变化测点B主应力走势基本一致;在量值上,拱形进洞法的小主应力较门形进洞法的略大,但都很小,隧道全部贯通后,门形与拱形进洞法小主应力值分别保持在-0.05 MPa、-0.10 MPa。测点C在交叉段拱腰,其主应力随开挖步序的变化与交叉段拱顶测点B基本一致。对交叉段边墙测点D展开分析,风道上台阶开挖对其基本没有影响,交叉段上台阶开挖导致大主应力快速增大,门形进洞法增大到-1.05MPa,拱形进洞法增大到-1.72MPa,小主应力有轻微减小;主体隧道上台阶开挖导致门形进洞法和拱形进洞法增大量相当,约为0.30MPa,小主应力基本不变;风道段与主体段下台阶开挖对大、小主应力影响都很小;交叉段下台阶开挖使大、小主应力骤减,门形进洞法大主应力减小至-1.04 MPa,拱形进洞法大主应力减小至-0.83 MPa,而门形进洞法和拱形进洞法小主应力均减小至-0.25MPa左右,开挖通过边墙测点时均会引起大主应力显著减小。
可见单向拱和穹拱形施工引起的应力值相当,但是单向拱测点A、B的小主应力出现拉应力,这对安全是不利的,从控制交叉段围岩应力状态的角度出发,双向拱更有利于控制隧道围岩的稳定性。
4.2 模型试验验证分析
结合模型试验现象及数值计算数据,对内拐角围岩应力随施工过程演化情况进行分析,如图11所示。内拐角测点大主应力方向为竖向,小主应力方向水平。由图11可知,上台阶开挖过程中,大主应力逐渐增大,由-0.95MPa递增到-1.39MPa,而小主应力变化趋势相反,由-0.52MPa递减至-0.09MPa。随着下台阶的开挖,内拐角围岩应力状态呈现出“三向—两向—单向”的变化趋势,围岩小主应力由压应力-0.18 MPa变为交叉段下台阶开挖后的0MPa,隧道开挖完成后变为拉应力1.91MPa。这种三向变单向的应力状态变化严重威胁着隧道安全,模型试验开挖结束后内拐角部位围岩出现裂隙,因此内拐角是交叉隧道施工过程中需重点关注的部位。

图11 交叉段内拐角处围岩应力演化过程示意
模型试验应变监测数据如图12所示,其中负值为压应变。测点1和2位于靠近风道侧,受开挖影响较早,在风道开挖阶段其应变分别增长1150με和1 620 με。交叉段开挖对各监测点影响较小,主体段开挖各测点应变值均有明显增加,随后保持稳定。由于应力集中,内拐角拱脚测点2应变值最大,稳定在-3000 με,拱顶测点3最小,稳定在-1400με,与数值计算围岩受力特点规律一致。
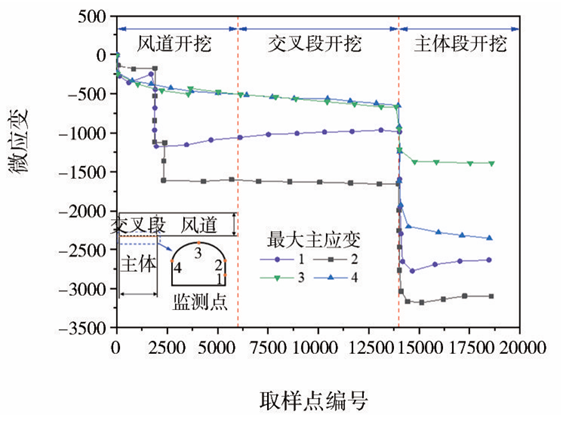
图12 模型试验应变监测值
5 支护作用下穹拱结构受力特点分析
5.1 围岩位移
穹拱结构监测断面位置如图13所示,各断面竖向位移云图如图14所示。由图14可知,风道距交叉段较远(2倍风道洞径)位置处和主体隧道距交叉段较近(1倍主体隧道洞径)位置处,竖向位移呈现对称分布,但随着距离交叉段越近,竖向位移分布逐渐趋于不对称。主体段受交叉隧道影响区域小于风道段,但主体隧道拱顶沉降量大于风道段,这是由于主体隧道断面较大,围岩应力重分布程度更剧烈。
图13 监测断面位置
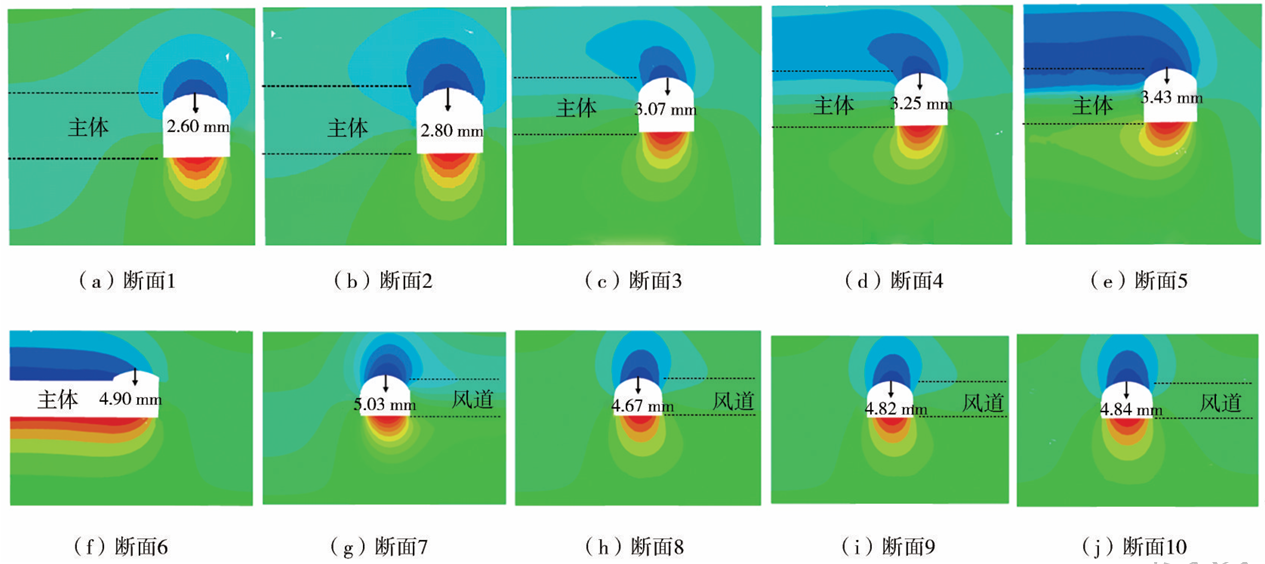
图14 穹拱结构不同监测断面隧道围岩竖向位移云图
穹拱结构拱顶沉降曲线如图15所示,可知当隧道开挖至断面位置时,各断面均产生明显沉降,越靠近交叉段的断面沉降量越大。风道中各断面的沉降主要发生在风道拱部和交叉段拱部开挖时,主体段断面的沉降发生在交叉段拱部和主体段拱部开挖时,隧道下台阶的开挖对拱顶沉降影响很小。交叉段内测点最终沉降值稳定在3.07mm,小于风道段的3.30 mm和主体段的5.03mm,说明交叉段采用穹拱结构对沉降控制有较好的效果。
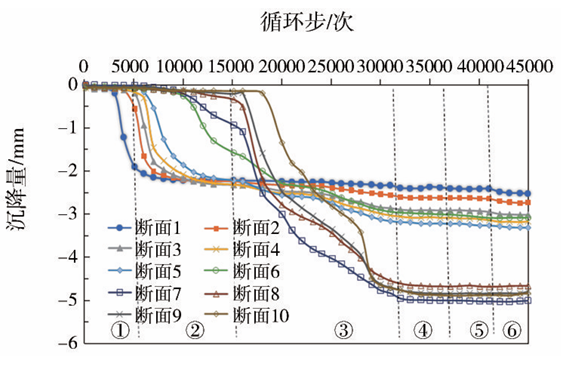
图15 穹拱结构拱顶沉降曲线
5.2 围岩应力
监测断面7位于交叉段主体侧,各测点应力变化曲线如图16所示,图中负值代表压应力。由图16可知,拱顶测点3的主应力最小,仅在交叉段拱部和主体段拱部开挖时产生波动,大主应力保持在-0.5MPa左右。内拐角测点4和5在交叉段上台阶开挖时应力分别增大至-1.3MPa和-1.7MPa,随后保持稳定,在交叉段下台阶开挖时应力值减小,而主体段下台阶开挖时又指数式增大至-2.8MPa左右,并且小主应力由压应力变为拉应力,分别达到1.4MPa和2.0MPa。下台阶开挖过程中外拐角测点应力变化与内拐角相反,隧道开挖完成后测点1和2的应力值分别减小至-0.8 MPa和0 MPa。随着下台阶的开挖结束,荷载由外拐角转为内拐角围岩承担,内拐角围岩应力水平高,大主应力方向受压,小主应力方向受拉,不利于围岩承载。
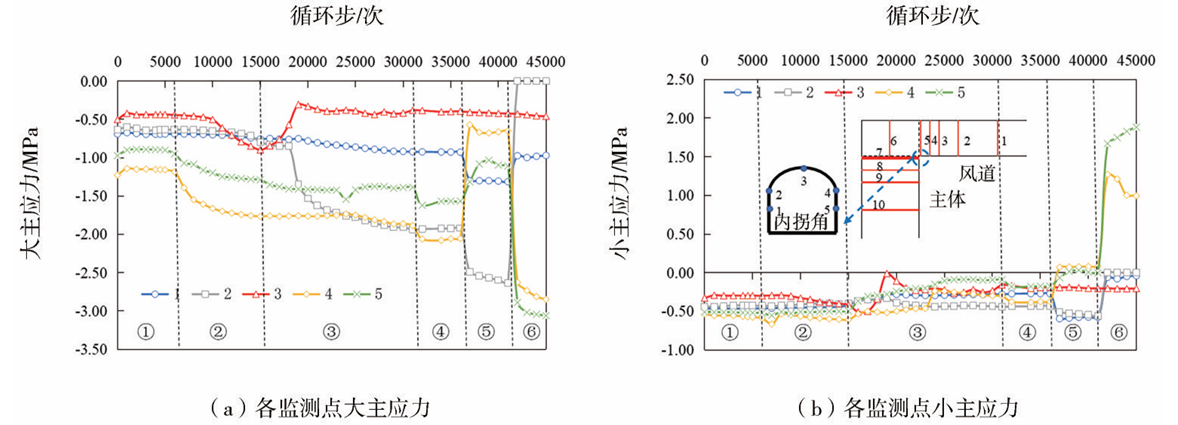
图16 断面7各测点的应力变化曲线
5.3 支护结构受力
(1)喷层
地铁暗挖车站风道-主体交叉段喷层大小主应力云图如图17所示,图中大主应力为压应力,小主应力为拉应力。最大压应力位置在交叉段内拐角拱脚处,其值为10.86MPa。拉应力最大位置在交叉段与主体隧道和风道的交叉截面处,最大拉应力为0.11MPa,特别是交叉段内拐角和交叉段-主体交叉截面位置处,应力集中程度高,与围压应力分布规律一致。在实际工程中需要对交叉段内拐角位置加强支护。
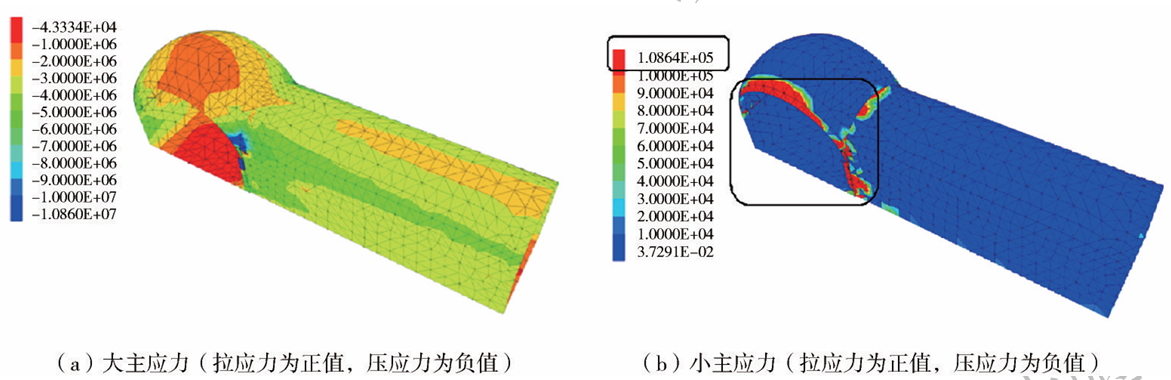
图17 交叉段喷层主应力云图(单位:Pa)
(2)锚杆
风道段采用中空注浆锚杆,交叉段与主体段采用100 kN的预应力锚杆,隧道开挖后锚杆轴力云图如图18所示。可知风道段中空注浆锚杆轴力较小,均不超过4kN,主体段与交叉段锚杆相对风道段锚杆受力更大,主体段锚杆轴力为50kN左右。

图18 风道段锚杆轴力云图(单位:N)
断面1内锚杆轴力变化如图19(a)所示,可知开挖隧道拱部阶段,锚杆轴力保持稳定,锚杆3轴力最大为2kN,其余锚杆几乎不受力。在开挖风道下台阶时除锚杆3外其余锚杆轴力均有增加,锚杆1和5轴力分别增加至3.3kN和3.6kN,锚杆2和4轴力增加至0.8kN和1kN左右。主体段中典型断面8锚杆轴力如图19(b)所示,锚杆轴力在整个开挖过程基本保持稳定,其中拱顶位置锚杆轴力最大,其值为54.9 kN,左右拱脚位置锚杆轴力为42.2kN。
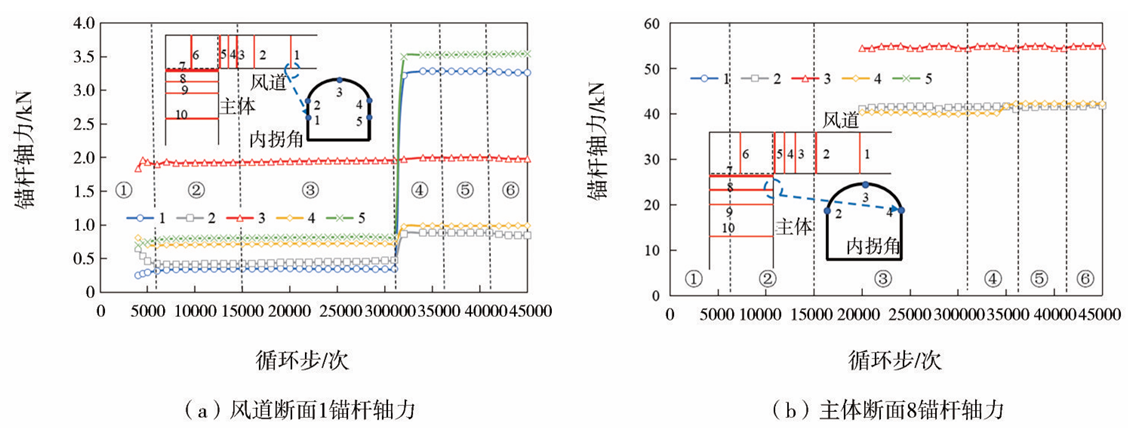
图19 风道段锚杆轴力曲线
综上所述,下台阶开挖对风道段边墙位置中空注浆锚杆影响最大,锚杆轴力变化量约占最终值的77.18%~89.57%,保持较高的工作轴力;预应力锚杆轴力基本不受开挖过程的影响。
(3)格栅钢架
格栅钢架的受力云图如图20所示,可知主体段与风道段格栅钢架受力相近,均受压,内拐角位置处所受的压力值最大,为266.7kN;交叉段靠近主体侧部分格栅钢架受拉,最大拉力值为76.6kN。
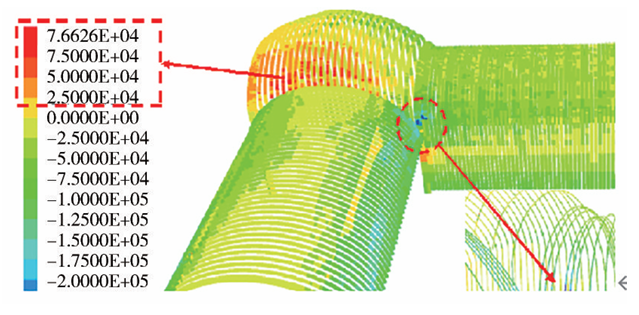
图20 格栅钢架轴力云图(单位:N)
典型断面5和8不同位置拱架轴力变化曲线如图21所示。由图21(a)可知,断面5内各测点拱架轴力在施作拱架后明显上升,开挖全过程中拱架轴力最大值均出现在内拐角侧拱脚位置,开挖完成后拱架轴力约-150kN。拱部拱架轴力最小,约为-20kN,断面内拱架受力与围岩受力分布规律一致。由图21(b)可知,断面8仅有拱部设置拱架,同断面5一致,拱架轴力最大值位于内拐角侧,但断面8拱顶拱架轴力大于外拐角拱脚位置,拱架受力呈现明显的不对称性。
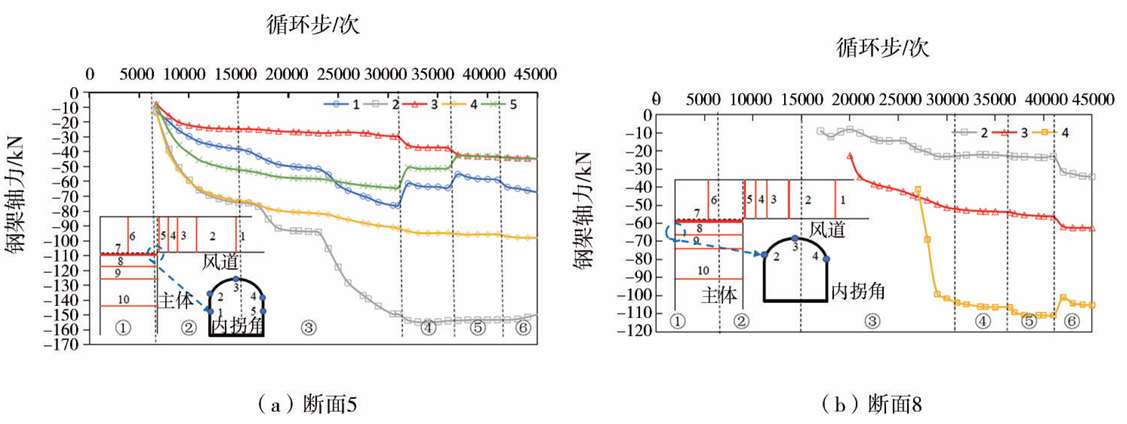
图21 格栅钢架轴力曲线
交叉段靠近主体侧钢拱架出现受拉,分析认为是由于在开挖主体前破除了交叉段主体侧的格栅钢架,后架设主体钢架时,挑高段钢架缺乏支撑,因此出现拉力,对隧道的稳定极为不利。基于此,提出了“先支后破”的施工工法,即在破除交叉段钢架前架设内套钢架,横通道挑高段开挖完成后,用于支撑横通道拱部格栅钢架,避免后期格栅钢架凿除时挑高段拱部悬空,如图22所示。通过两种设计方案对比,发现优化后的设计方案的喷射混凝土用量可减少25%以上,格栅钢架用量可减少35%以上,且施工效率也可大幅提升,总体具有较为显著的经济效益。
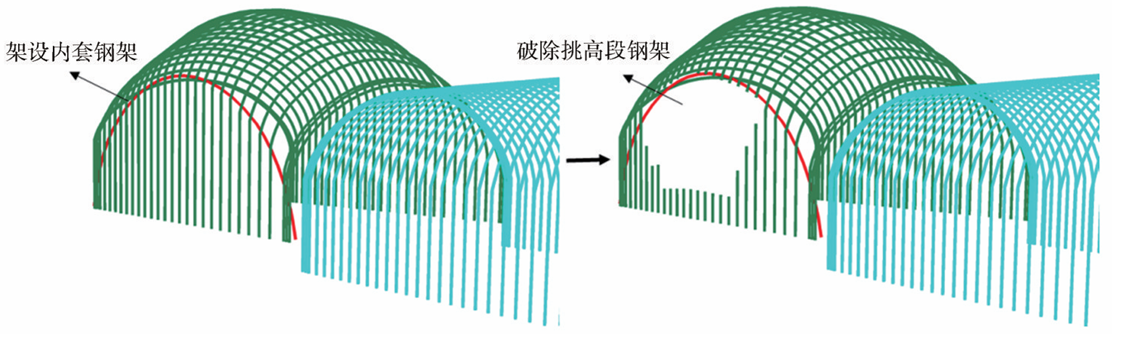
图22“先支后破”施工工法示意
6 工程实践
在项目现场对地表沉降、拱顶沉降、锚杆轴力、格栅钢架应力进行监测。监测断面位置及各断面测点位置如图23所示。
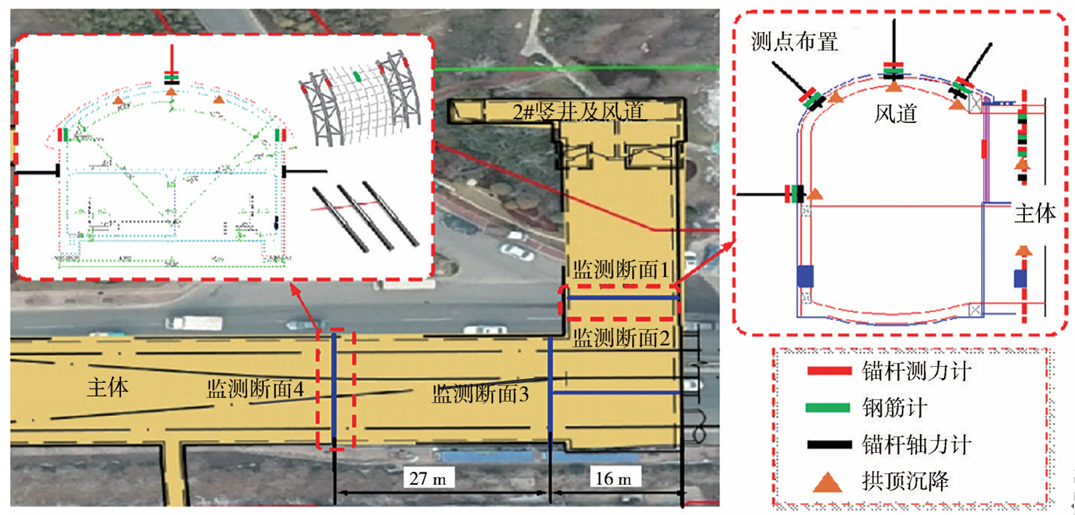
图23 监测断面及测点布置示意
现场监测的地表沉降曲线如图24(a)所示,可知曲线整体呈现台阶式变化趋势;断面1受交叉段及主体段开挖扰动,有2次台阶式增长,在开挖后200 d稳定在13.1 mm;断面2和3变化趋势相同,最终稳定在8mm左右,小于断面4的10.3mm。
现场监测的拱顶沉降曲线如图24(b)所示。可知由于交叉段的多次开挖影响,监测断面1的拱顶沉降波动次数和幅度最大,断面1拱顶沉降到达稳定所需的时间最长,135d后稳定在6.3mm;监测断面2在32d时稳定在5.3mm,受其他部位开挖影响较小;断面3拱顶沉降在开挖后28d到达第一个平台,沉降量1.3mm,40d时受开挖影响产生波动,10d内累计变化量为1.2mm,沉降稳定在2.5mm;监测断面4在第12d就稳定在3.2mm。
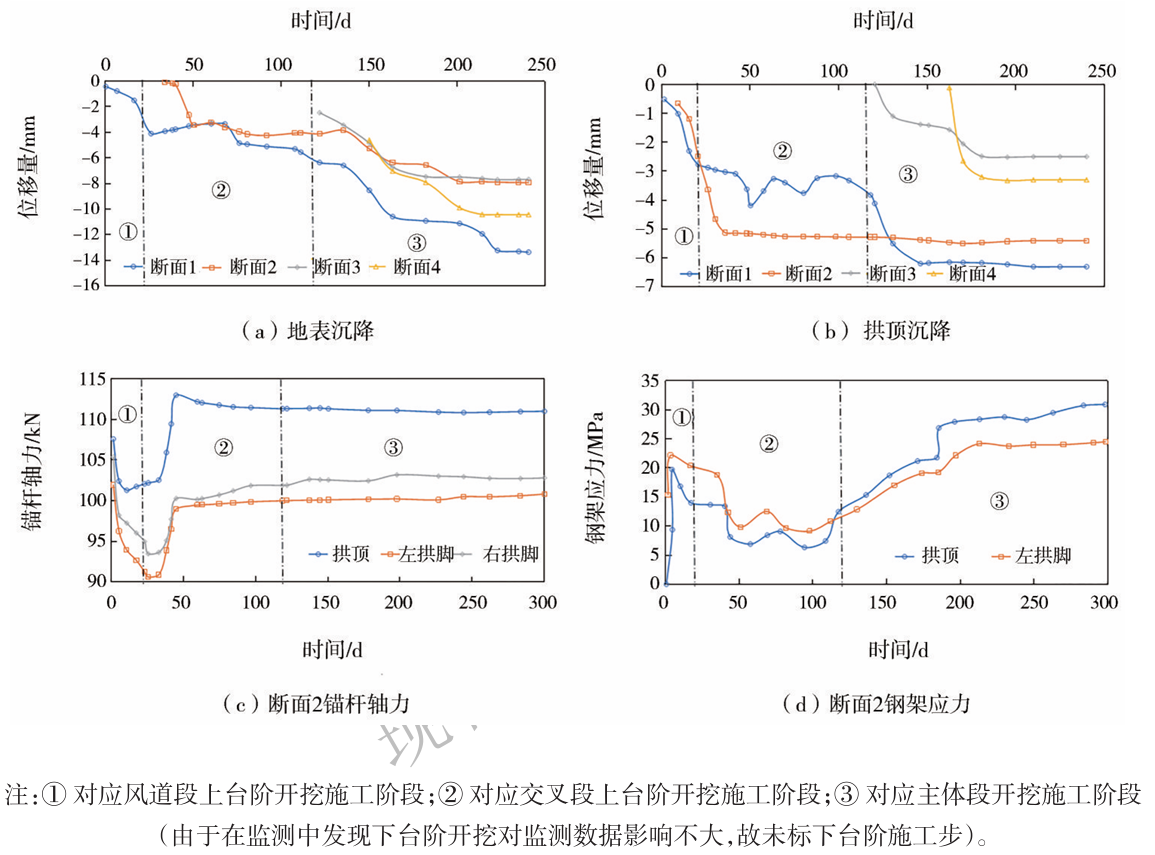
图24 现场监测结果
现场监测的断面2锚杆轴力曲线与钢架应力曲线如图24(c)、图24(d)所示。可知轴力总体上呈“减小—增大—稳定”的变化趋势。分析认为在锚杆监测前50d受隧道爆破开挖扰动影响,锚杆轴力出现变化,隧道受开挖的影响减小,锚杆轴力保持稳定,最终稳定在103kN左右。由于断面2开挖时间较早,受后续开挖扰动明显,钢架应力曲线呈现“增长—下降—增长—趋稳”的变化趋势,钢架应力最终稳定在30MPa左右。
综上所述,隧道拱顶最大沉降仅为6.2mm,锚杆轴力、钢架应力均小于其屈服强度,围岩整体稳定。现场所用支护参数及“先支后破”施工工法有效保证了穹拱形地下结构的稳定性。
7 结 论
(1)相较于单向拱洞型,隧道交叉段穹拱形洞型更有利于围岩稳定,拱顶沉降量更低,减少约7%。
(2)对比单向拱和穹拱形结构围岩的应力发现,由施工引起的应力值几乎相当,但是单向拱内拐角处小主应力出现拉应力,对围岩极为不利,因此双向拱更有利于控制隧道围岩稳定性。
(3)穹拱形洞型内拐角围岩应力状态在开挖过程中呈现“三向—两向—单向”的变化趋势,这种三向变为单向的应力状态变化对隧道安全不利,且此处围岩出现裂隙,因此在施工过程中应重点关注交叉隧道的内拐角部位。
(4)在支护作用下,围岩位移与应力呈现出与毛洞状况下相近的变化趋势;喷层拉应力最大值达到0.11 MPa,位于交叉段内拐角和交叉段-主体交叉截面位置处,且应力相对集中,因此应在实际工程中对交叉段内拐角位置加强防护;下台阶开挖对风道段边墙位置中空注浆锚杆影响最大,工作轴力较高,而预应力锚杆轴力基本不受此过程的影响。
(5)拱架受力呈现明显的不对称性,交叉段靠近主体侧钢拱架出现受拉,针对交叉隧道拐角处容易出现应力集中及拉应力区、交叉段主体侧支护结构受力较大的问题,提出了破除格栅钢架前架设内套钢架的“先支后破”施工工法,同时此工法可减少喷射混凝土用量约30%,减少格栅钢筋用量约35%,施工效率整体提升50%以上。
(6)现场监测显示,采用了“先支后破”施工工法的穹拱形隧道拱顶最大沉降量在5.2mm左右,支护结构受力均在安全范围内,隧道整体稳定。
摘自《现代隧道技术》