1 引 言
盾构法具有施工速度快、施工质量高、地表沉降小等特点,被广泛应用于城市轨道交通的建设中。然而,随着盾构掘进环境的水文地质情况愈加复杂,盾构隧道在施工过程中不可避免地会穿越桥梁或建构筑物群桩。盾构隧道穿越群桩时,会造成群桩额外的内力和位移场,降低桩的承载力,这种情况在软土地基中尤为严重。当桩基侵入隧道线路且难以调整线路时,最简单快捷的策略是采用桩基托换拆除原有桩基,然后盾构机直接切割原有钢筋混凝土桩,以减少对既有上部结构的影响。
目前,盾构切桩法仍然是一项前沿技术,随着盾构技术的快速发展,盾构机直接截桩的工程案例越来越多。大多数研究主要运用数值计算、理论分析、模型试验等方法分析盾构机侧穿邻近桥梁或者建筑物桩基的影响。He等采用非线性有限元模拟盾构掘进过程中邻近群桩的变化过程,研究了群桩与隧道中线的最小距离对群桩响应的影响。王德福采用滚刀-桩基-地层动态切削仿真模型,分析了盾构切削桩基过程中滚刀间距、刀圈贯入度、刀盘转速以及桩基相对刀盘的位置等关键参数的敏感性,并给出了滚刀切桩的最优参数值。此外,Xu等通过实际工程案例,提出了桩基托换后盾构机直接切桩的施工方案。
从本质上讲,盾构切削钢筋混凝土桩基的过程是盾构刀具与钢筋混凝土之间的动态接触过程,刀 具切削混凝土的过程与刀具切削岩石的过程极其相 似。大量研究人员利用数值建模的手段分析了盾 构刀具的破岩过程。Duan等基于有限元法模拟 了岩石破碎过程,研究了刀具的几何构形对岩石破 碎行为的影响,包括刀刃的宽度与刀刃的圆角。 Stopka运用 LS-DYNA非线性动力学软件内置的 DEM(Discrete Element Method)工具模拟了非对称 盘形滚刀切割岩石的过程,研究结果表明,DEM建 模方法可以用来分析盘形滚刀破岩或采矿等复杂的 动力学过程。龚秋明等利用自主研发的滚刀破岩 室内试验系统,开展了不同刀刃形式下的盘形滚刀 破岩试验,基于岩石破碎照片以及滚刀受力数据讨论不同刃形滚刀的适用性。
然而,由于混凝土中钢筋的影响,包括钢筋与混凝土之间复杂的相互作用,刀具切削钢筋混凝土结构与切削岩石的最大区别及难题在于混凝土中钢筋的切割,目前针对这一方面的研究较少。随着数值算法的进一步发展与改进,更多的研究人员认为混凝土不能被看作连续的介质,其自身的物理力学特性可以用离散元法进行描述;混凝土中的钢筋可以被看作连续介质,其物理力学特性可以用有限元法来模拟。
本文研究利用有限元-离散元耦合的方法(FEM-DEM,Finite Element Method-discrete Element Method)分析滚刀切削钢筋混凝土的瞬态动力学过程。在FEM-DEM耦合模型中,混凝土的力学行为通过离散元方法来描述,混凝土中钢筋的物理力学特性通过有限元方法来模拟。此外,数值模型计算结果的有效性与准确性通过室内试验进行验证。同时,分析盾构掘进参数对滚刀切削钢筋混凝土效果的影响,给出盾构掘进时的合理工作参数。
2 FEM-DEM耦合建模
2.1 DEM建模
离散单元法已被广泛应用于岩土工程、采矿工程与机械工程中。基于非连续介质力学理论,离散单元法可以很好地模拟材料复杂的破碎过程,例如混凝土材料或岩石材料与机器之间的动态接触。因此,离散元法可以用来描述钢筋混凝土桩基中的混凝土介质。在LS-DYNA计算程序中,为了描述混凝土颗粒间的力学行为,离散的颗粒间需要添加Bond键来描述,如图1所示。
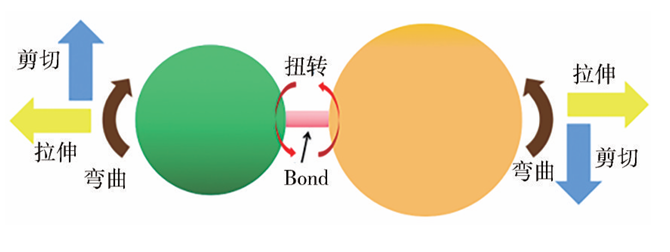
图1 相邻两个颗粒间的Bond键
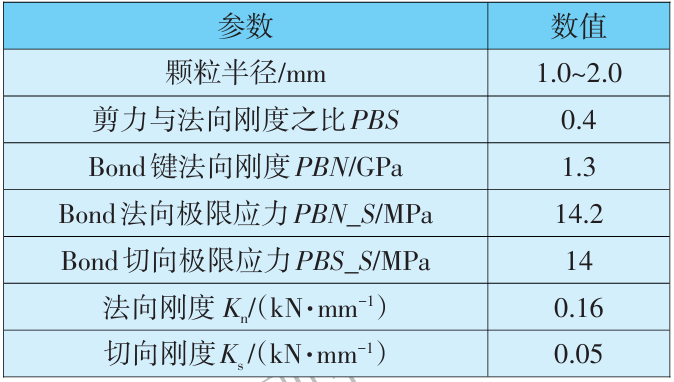
混凝土的宏观物理参数不能直接转换成DEM 中的接触参数。因此,有必要使用标定的方法来确 定一组合适的接触参数,这些参数是通过比较DEM 模拟结果和材料特性试验来确定的。本文分别采用 单轴压缩试验和巴西劈裂试验来标定DEM中的混 凝土接触参数。根据已有研究,刀具尺寸与颗 粒直径之比应不小于10。综合考虑模拟精度和计 算成本,混凝土颗粒的半径确定为1.0~2.0mm。试 验用混凝土的密度为2130kg/m3,单轴压缩强度为 23.7 MPa,劈裂强度为2.3MPa,杨氏模量为1.6GPa, 泊松比为0.275。在Stopka研究的基础上,确定了 混凝土颗粒之间的一组合适的接触参数。混凝土 的单轴压缩试验和巴西劈裂试验的力与位移关系 如图2(a)、(b)所示。可知数值模拟与室内试验的 压缩强度有一定偏差,产生这一现象的原因是研究 中使用的单相DEM模型将混凝土非均质混合物简 化为均质材料,忽略了不同组分之间明显的相互作 用。数值模拟与室内试验中的单轴压缩与巴西劈裂 试验的失效模式如图2(c)所示,可知数值模拟和实 验室测试中的混凝土样品呈现出非常相似的断裂模 式,大量剪切和拉伸裂纹扩展和聚结,导致样品最终 断裂。尽管数值模拟与室内试验的压缩强度有一定偏差,但数值模拟中材料的抗压和劈裂模式非常相似。因此,建立的颗粒模型可以描述实际的混凝土力学行为(C25)。标定后的混凝土颗粒接触参数结果设置见表1。
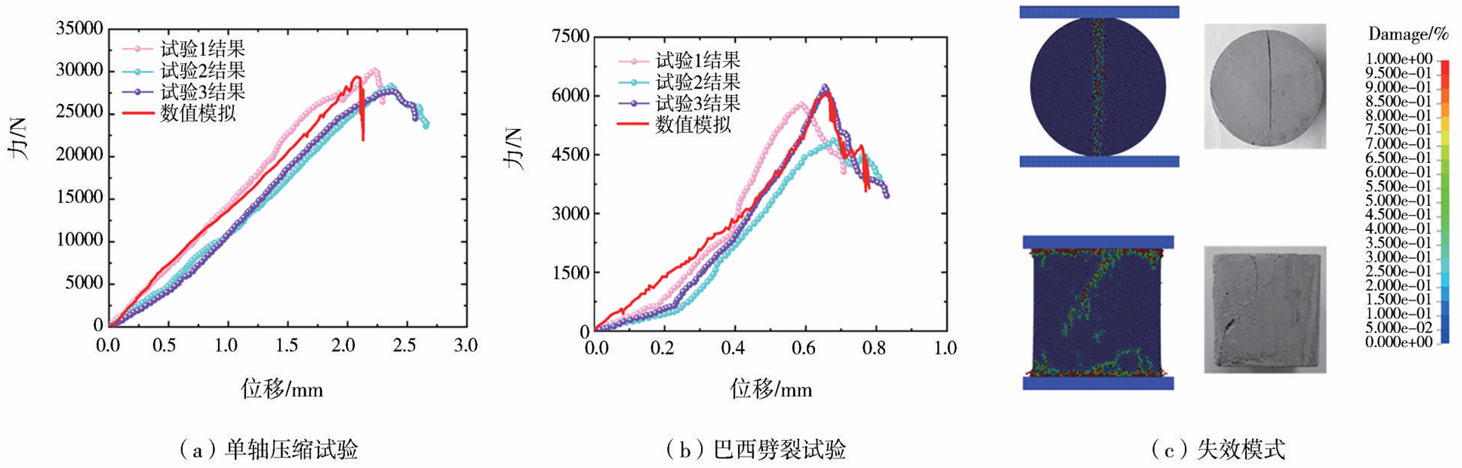
图2 室内试验结果与数值模拟结果对比
表1 DEM模拟中实际参数设置
2.2 FEM建模
有限元建模过程中,运用Johnson-Cook(J-C)材料模型和失效模型来描述钢筋的物理力学行为,J-C模型在描述金属材料的大应变、高应变率以及高温下的强度极限和破坏过程方面具有显著的优势。其材料模型的应力方程为:
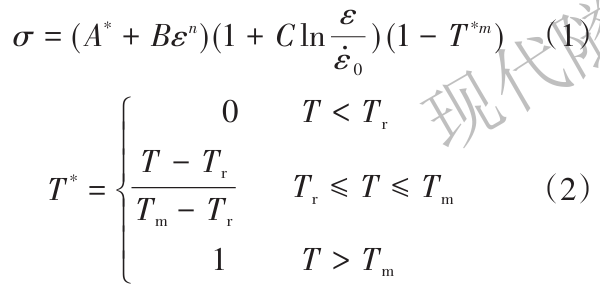
式中:σ为有效应力;ε为等效塑性应变;ε为等效塑性应变率;ε0为参考应变率;T*为同系温度;T为材料的当前温度;Tr为室温;Tm为材料的熔点温度。J-C方程材料常数为标准条件下材料的屈服应力A*、应变硬化变量B、应变速率的强化因子C、应变硬化因子n和热软化系数m。本文在数值模拟中没有考虑温度的影响。此外,J-C失效模型假设损伤参数D>1时出现材料失效,损伤参数D为:
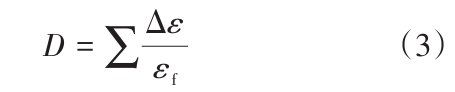
式中:Δε为等效塑性应变增量;εf为失效应变,其表达式为:
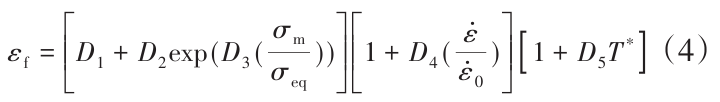
式中:D1 ~D5分别为材料损伤类形常数;σm为平均应力;σeq为等效应力。
盘形滚刀采用弹塑性本构模型,如图3所示。为了节省计算资源,只建立了盘形滚刀刀圈。采用侵蚀面-面接触算法描述滚刀刀圈与钢筋的相互作用,圆盘刀环与钢筋的静摩擦系数为0.2,动摩擦系数为0.15。钢筋和滚刀刀圈的力学参数见表2,钢筋的J-C模型参数见表3。
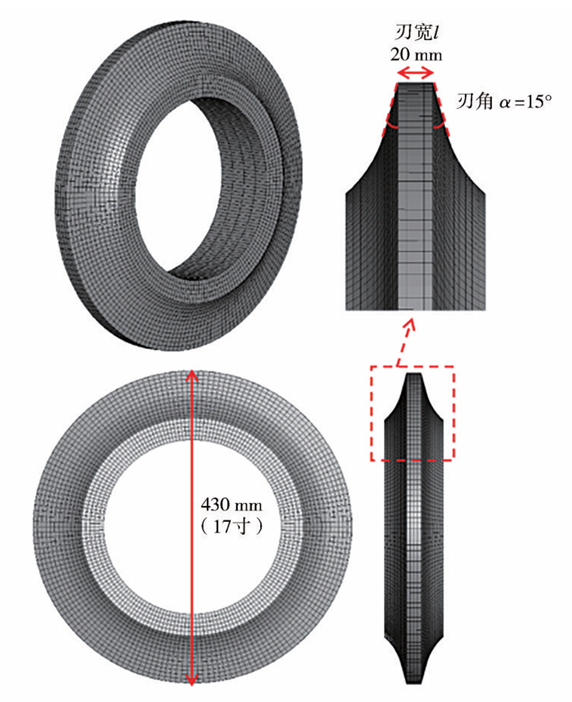
图3 滚刀刀圈几何模型示意
表2 钢筋与滚刀刀圈力学参数
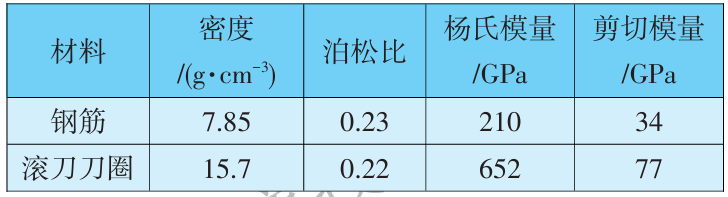
表3 钢筋的J-C模型参数设置

2.3 边界条件设置
采用基于罚函数的算法来实现离散元粒子与有限元节点的相互作用。DEM颗粒和FEM单元之间耦合方法的原理如图4所示,主要步骤为在时间增量开始时,检查FEM节点和DEM颗粒之间的界面。如果发生穿透,则产生FEM表面与DEM颗粒之间的接触力。此外,还需要更新FEM和DEM的参数。由于有限元法和离散元法的稳定性时间步约束不同,因此有必要确保耦合过程中两个时间步ΔtFEM与ΔtDEM相同,并确定适当的全局时间步ΔtFEM-DEM。因此,在同一计算框架下,每一步的时间增量应相等,即:
ΔtFEM- DEM= min( ΔtFEM,ΔtDEM) (5)
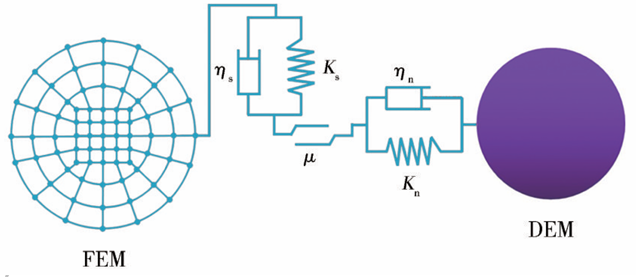
图4 FEM-DEM耦合方法原理
DEM颗粒用于模拟混凝土,钢筋和滚刀刀圈采用FEM方法模拟,其静态和动态摩擦系数设置为0.3,从而实现盘形滚刀切削钢筋混凝土桩的数值模拟。在模拟过程中,耦合模型右侧(y方向正向)、左侧(y方向负向)和底部(z方向负向)采用固定边界,而其他侧设置为自由边界,钢筋距离上侧边界的距离为5mm,并处于x方向的中间位置,如图5所示。FEM-DEM耦合计算工况设置见表4,所有耦合计算均在标准台式计算机上运行(第13代英特尔酷睿i7-13700KF、3.40 GHz × 24和64GBRAM)。
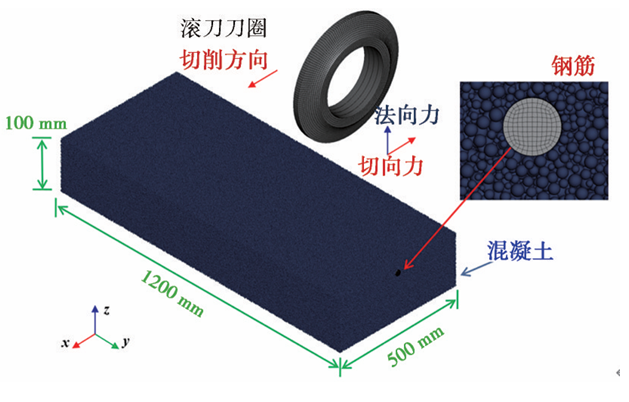
图5 FEM-DEM耦合全局模型
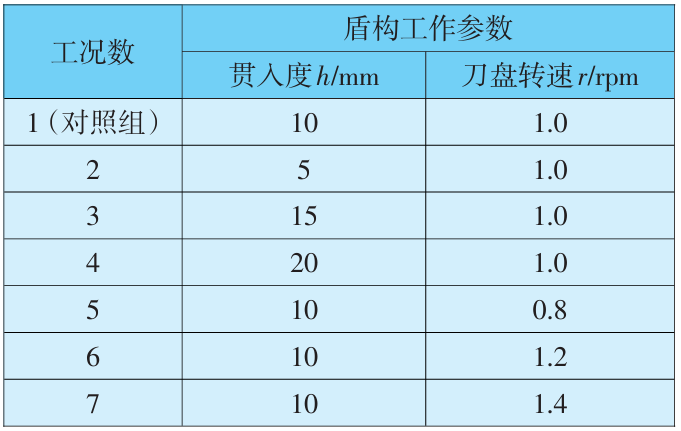
表4 耦合计算工况
3 结果与分析
3.1 滚刀切削钢筋混凝土桩动力学分析
混凝土颗粒和钢筋的损伤直接反映了盘形滚刀的性能。以对照组为例,不同时刻数值模拟获得的混凝土颗粒损伤分布云图如图6所示。由图6可知,与远离盘形滚刀的区域相比,靠近盘形滚刀的区域 的混凝土颗粒的损坏相对较高。在盘形滚刀与混凝 土接触初期(30ms),损伤区深度约等于盘形滚刀的 切入深度,损伤区宽度略大于盘形滚刀的刀刃宽度, 约为刀刃宽度的1.5倍。随着盘形滚刀的继续切割 (60 ms),混凝土损坏区的深度和宽度都增加。此 外,值得一提的是,当盘形滚刀切割到钢筋附近时 (150 ms),混凝土损伤区的宽度突然增加到大约贯 入度的4倍。这是因为混凝土对钢筋的约束已经失 效,钢筋在盘形滚刀的切割作用下出现明显的弯曲 变形,导致其周围的混凝土被压碎。
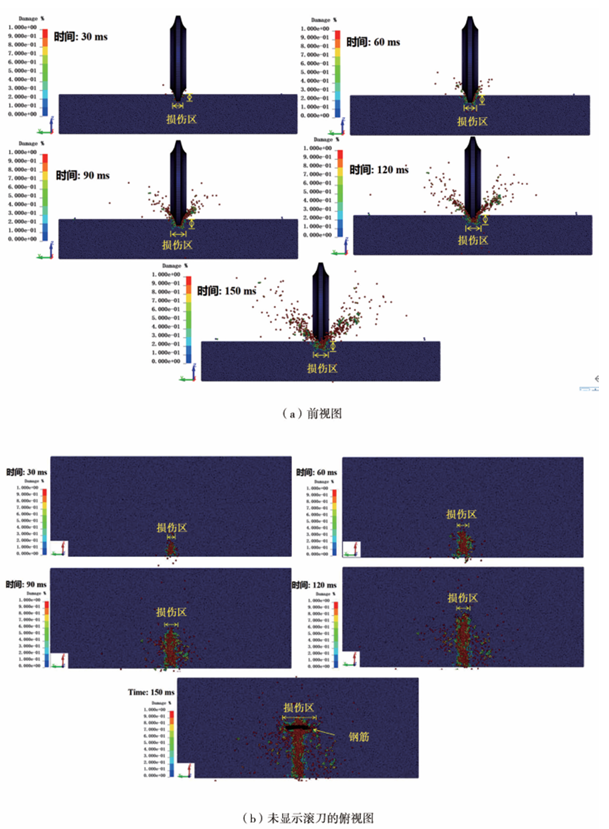
图6 不同时刻混凝土颗粒损伤分布云图
不同时刻数值模拟获得的钢筋损伤分布前视图如图7(a)所示。由图7(a)可见,当盘形滚刀靠近钢筋但还未接触时(130ms),钢筋表面的局部损伤已经发生,宽度约为24mm。这是因为靠近钢筋的混凝土在盘形滚刀的切割作用下被压碎,导致钢筋受到挤压。当钢筋与盘形滚刀初始接触时(138ms),损伤区宽度进一步扩大到约30mm,钢筋发生轻微的弯曲变形。当切割时间增加到150ms时,盘形滚刀切割的区域中部分钢筋单元失效并被移除,在钢筋表面上留下类似梯形的切割痕迹。随着切割时间的增加(152~156 ms),钢筋发生了显著的弯曲变形,受拉侧(下侧)的应力已经超过了钢筋的极限抗拉强度,导致钢筋受拉侧出现了初始断裂。并且裂缝继续扩大,最终钢筋的下部整体断裂,可以观察到钢筋上表面的损伤区宽度增加到48mm,约为盘形滚刀刀刃宽度的2.5倍。
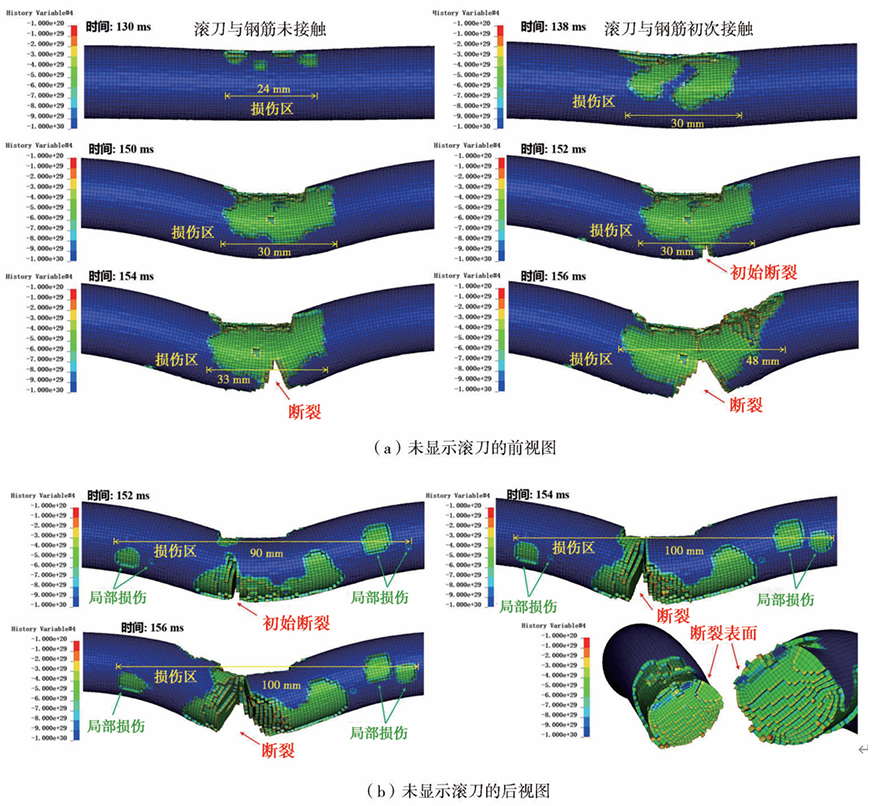
图7 不同时刻钢筋损伤云图分布云图
为了进一步说明钢筋受拉侧损伤模式的变化,钢筋的后视图和断裂截面上的损伤分布如图7(b)所示。可以观察到,钢筋拉伸侧的损伤区宽度约为100 mm(约为刀刃宽度的5倍),钢筋拉伸区的边缘有局部损伤,钢筋的断口比较粗糙,断口上有清晰的颗粒状和纤维状断口形貌。这是一种典型的延性破坏,即钢筋会发生显著的塑性变形,最终在拉伸过程中断裂,且断裂面较为粗糙。
盘形滚刀的切向力-时间曲线和法向力-时间曲线分别如图8、图9所示。从图8可以看出,盘形滚刀切向力呈现先快速增加,然后减小,最后稳定的趋势,在切割混凝土期间,平均值约为12.1kN;当切削到钢筋时,切向力突然增大,峰值约为225kN。随后,在钢筋断裂的瞬间,盘形滚刀承受的冲击力急剧下降。这是由于相较于混凝土,钢筋的硬度更高,当刀具与钢筋接触时,刀具受到钢筋的冲击荷载作用,因此盘形滚刀切削力突然增大,当钢筋断裂的瞬间,刀具与钢筋之间的相互作用消失,因此滚刀切向力急剧下降。值得注意的是,在最大峰值之前还有一个大约100kN的切向力峰值,这是因为钢筋本身的硬度高于混凝土的硬度,具有较高转速的盘形滚刀在其与钢筋接触的瞬间产生较大的负加速度,即盘形滚刀受到由钢筋施加的冲击荷载。
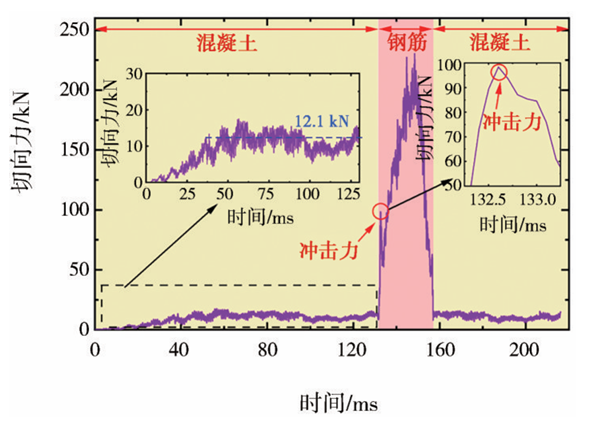
图8 盘形滚刀切向力-时间曲线
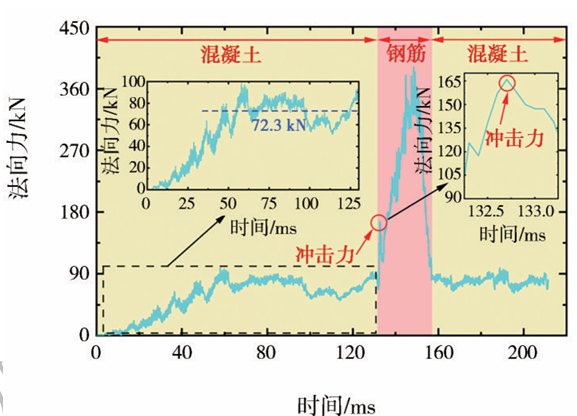
图9 盘形滚刀法向力-时间曲线
通过对比图8和图9可知,法向力-时间曲线具有与切向力-时间曲线一致的趋势,并且法向力的发展阶段与切向力的发展阶段一致。盘形滚刀在切割混凝土时法向力的最终稳定值为72.3kN,在切割钢筋时法向力的峰值约为400kN。
3.2 模型有效性验证
为了验证FEM-DEM耦合模拟结果的准确性和可靠性,设计了盘形滚刀切削钢筋混凝土桩的试验装置,并进行室内试验,切削试验平台主要由液压系统,加载系统(X轴油缸驱动,Y轴伺服调整,Z轴压力加载系统),数据检测采集系统,反力架,试件台,换刀装置,控制台,液压站,液压控制电控柜,配电箱等组成,如图10所示。其中,法向力加载系统可提供50 t最大垂直力,切向驱动系统可提供20t最大切削力。

图10 盘形滚刀切割钢筋混凝土试验装置
对比试验测量的切削力和FEM-DEM耦合模拟测量的切削力,结果如图11所示。总体而言,数值模拟结果与试验结果吻合较好,证实了有限元-离散元法模拟盘形滚刀切削钢筋混凝土桩的适用性。在大多数情况下,有限元-离散元模拟与试验得到的切削力和法向力的差值均小于10%。尽管FEMDEM模拟结果和试验结果在个别点上存在差异,但FEM-DEM模型提供了盘形滚刀的动力响应,响应结果相对令人满意。同时,Stopka等[指出FEMDEM方法可以很好地预测刀具切削混凝土时的受力,并经过了试验验证。因此,FEM-DEM模型可用于研究盘形滚刀切削钢筋混凝土桩的动力响应。
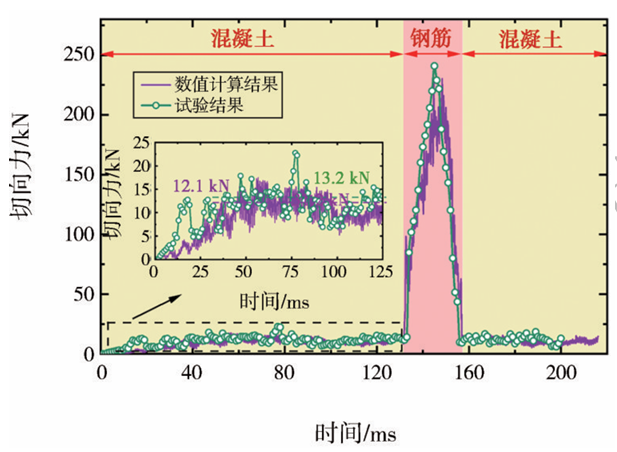
图11 室内试验与有限元-离散元耦合仿真测量切削力的比较
4 参数分析
4.1 贯入度对滚刀切桩性能的影响
不同贯入度下盘形滚刀切削力的时间历程曲线如图12(a)所示。可知在所有情况下,在切割混凝土范围开始时,切削力迅速增加,随后增长缓慢,并稳定在一个略有波动的范围。当盘形滚刀切削到钢筋时,切削力急剧增加,在所有情况下,盘形滚刀与钢筋接触的瞬间都存在冲击力。随后,在钢筋断裂的瞬间,盘形滚刀承受的力/负载急剧减小。此外,随着盘形刀具的贯入度增加,切削力-时间曲线上移,即在切削混凝土时盘形刀具切削力的稳定值和峰值增加。同样,在切割钢筋时,切削力和冲击力的峰值随着盘形滚刀贯入度的增加而增加。
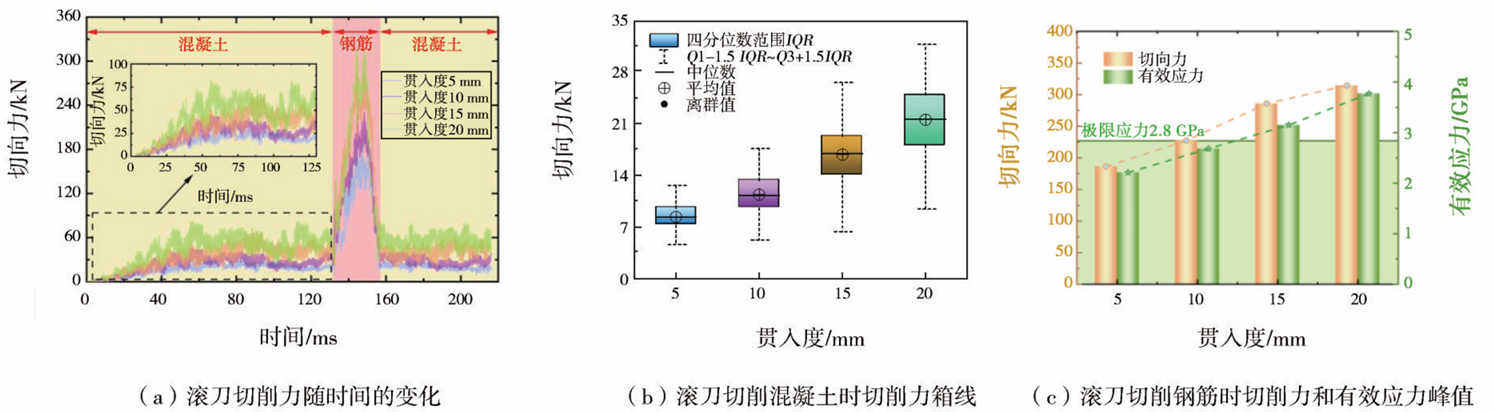
图12 不同贯入度下滚刀切削力与有效应力的变化
在切割混凝土期间绘制了4个盘形滚刀贯入度的切削力箱线图,如图12(b)所示,因为单个平均值可能会忽略时间历程中的变化,影响对结果的判断。从图12(b)可以观察到,切削力的平均值和波动随着盘形滚刀贯入度的增加而线性增加,这表明较高的贯入度会导致较大的切削力,高切削力意味着盾构刀盘的扭矩增加,会导致盾构机的掘进效率降低。在切割钢筋期间4个盘形滚刀贯入度下切削力和有效应力的峰值如图12(c)所示。可以看出,切削力和有效应力的峰值都随着盘形滚刀刀具贯入度的增加而线性增加。当贯入度大于15mm时,刀圈所受有效应力的峰值已经超过极限应力,导致刀圈开裂失效。据此可知,贯入度对盘形滚刀的切削性能影响显著,建议在盾构机切削钢筋混凝土桩时贯入度小于10 mm,避免刀圈断裂失效。
4.2 刀盘转速对滚刀切桩性能的影响
盘形滚刀在4种刀盘转速下切削力的时间历程曲线如图13(a)所示。切割混凝土期间4种刀盘转速下切削力箱线图如图13(b)所示。由图13(a)可知,盘形滚刀和钢筋之间的接触时刻随着刀盘转速的升高而提前,在所有情况下,切削力-时间曲线都有相似的变化趋势。与贯入度的增加相比,切削力-时间曲线随转速增加向上移动不明显,切削力平均值的增加相对适中,如图13(b)所示。这证明,与增加贯入度相比,在盘形滚刀切削混凝土期间,增加刀盘转速对切削力平均值没有显著影响。另外,由图13(c)可知,在盘形滚刀切割钢筋期间,切削力和有效应力的峰值增加也不明显。只有在非常高的刀盘转速(1.4rpm)下,刀圈的有效应力峰值才会超过极限应力。然而,值得一提的是,对于高刀盘转速(1.4 rpm),在盘形滚刀和钢筋接触的瞬间,盘形滚刀会受到更大的冲击力。因此,综合考虑盘形滚刀开裂失效和切削效率,盾构机切削钢筋混凝土桩时刀盘转速可适当提高,但在实际工程中不高于1.2rpm。
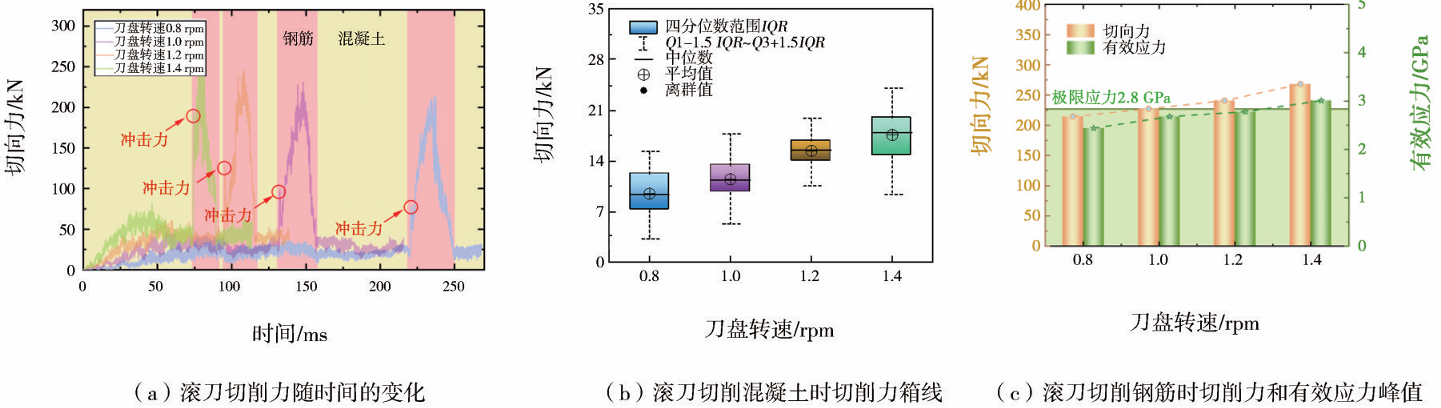
图13 不同刀盘转速下滚刀切削力与有效应力的变化
5 结 论
本研究利用有限元-离散元耦合的方法,分析了滚刀切削钢筋混凝土的瞬态动力学过程,数值模型计算结果的有效性与准确性通过室内试验进行了验证。同时,分析了盾构掘进参数对滚刀切削钢筋混凝土效果的影响,给出了盾构掘桩时的合理工作参数。具体研究结论如下:
(1)混凝土损伤区的最大深度和宽度分别是贯入度的2倍和刀刃宽度的1.5倍。由于混凝土对钢筋的约束已经失效,在盘形滚刀的切削作用下,钢筋表现出明显的弯曲变形,导致盘形滚刀切削到钢筋附近时,混凝土损伤区的宽度突然增大到4倍的贯入度。
(2)钢筋的损伤和断裂大致可分为3个阶段。在第一阶段,当盘形滚刀靠近钢筋但不接触时,钢筋表面的局部损伤已经发生。在第二阶段,在由盘形滚刀切割的区域中的部分钢筋单元失效并被移除,在钢筋表面上留下类似梯形的切割痕迹。在最后阶段,钢筋发生了显著的弯曲变形,受拉侧的应力已超过钢筋的极限抗拉强度,钢筋受拉侧出现初始断裂,最终钢筋整体拉伸断裂。
(3)根据参数分析,对于盾构工作参数,贯入度对盘形滚刀的切削性能有显著影响。与贯入度的增加相比,刀盘转速的增加对切削力没有显著影响。因此,在实际工程中,建议盾构机在切割钢筋混凝土桩时采用低贯入度、中等转速的掘进模式,建议贯入度小于10mm,刀盘转速低于1.2rpm。
摘自《现代隧道技术》