1 引 言
随着我国城市地下空间的不断完善,基坑近接既有地下结构的情况愈发普遍。基坑开挖会对周围土体产生扰动,从而引起既有地下结构产生附加位移及应力,特别是近接既有地铁运营隧道时,对基坑施工提出了更高要求。目前,国内外众多学者主要通过数值模拟、模型试验、理论分析、现场实测等方法,在基坑施工对既有结构力学特性影响方面做了大量研究,如既有车站及隧道的变形、邻近盾构隧道区间的受力,以及基坑施工引起的地表沉降等;对于新建地下结构的力学特征研究也非常常见,如地下连续墙的变形、弯矩、土压力,支护结构的应力等。魏纲等基于影像源法研究认为下卧隧道的隆起值与基底隆起值呈正相关关系。Zheng等研究了基坑开挖深度、围护结构水平位移和与隧道的相对位置对既有隧道位移响应的影响规律。Huang等通过模型试验研究表明隧道隆起量与隧道距基坑的距离呈指数递减分布。宗翔基于理论研究认为基坑开挖引起的隧道纵向位移随着其剪切刚度的增加而逐渐减小,最后收敛至一个稳定值。Liang等通过参数分析发现增加地层弹性模量将显著减小基坑开挖对盾构隧道的不利影响。魏纲等研究了基坑开挖对不同埋深下邻近地铁隧道的影响,认为随着隧道埋深的增加,其所受到水平、竖向附加荷载有所减小,隧道埋深大对保护隧道是有一定作用的。张治国等研究了基坑开挖对不同近接距离下隧道所受附加荷载的影响规律,结果明随着近接距离的增加,隧道所受竖向附加应力逐渐减小,地铁隧道的最大位移、最大弯矩逐渐减小。
以上研究均是将地层、隧道的参数作为影响因子进行单因素分析,如基坑开挖深度、基坑与隧道的相对位置、基底隆起、隧道剪切刚度、土体弹性模量、隧道埋深等。就基坑与隧道间的近接距离而言,一般认为随着近接距离的增加,隧道受基坑开挖的影响越小,产生的附加位移及附加应力等越小。然而,基坑与隧道的相对关系是复杂的,对于埋深较大的隧道(与基坑开挖深度接近),随着近接距离的增加,隧道受基坑开挖影响越小的结论是否同样适用有待进一步分析。所以,研究在近接距离与埋深的综合影响下隧道受到基坑开挖的影响规律是十分必要的。
本文依托北京地铁轨道交通新增换乘通道工程,首先,采用模型试验与数值模拟的方法,研究基坑开挖对既有隧道结构竖向位移的影响规律;其次,通过不同近接距离与埋深下的差异沉降,分析既有隧道结构的变形模式;最后,对近接距离与埋深两种影响因子进行综合分析,基于既有隧道结构的差异沉降提出了近接系数的概念,并对影响分区进行划分。
2 工程背景
北京轨道交通新增换乘通道工程宣武门站位于北京市二环以内的中心老城区,为4号线与2号线的换乘车站。自2009年4号线开通以来,因两线之间换乘设施通行能力严重不足,在早晚高峰期间大量乘客严重拥堵在换乘通道内,存在较大的安全隐患。为此,在东北方向增加北向出入口,以吸引宣武门内大街东侧客流。新增出入口总长约260m,其中售检票地下厅宽21.6m,长约37.13m,采用明挖法施工。
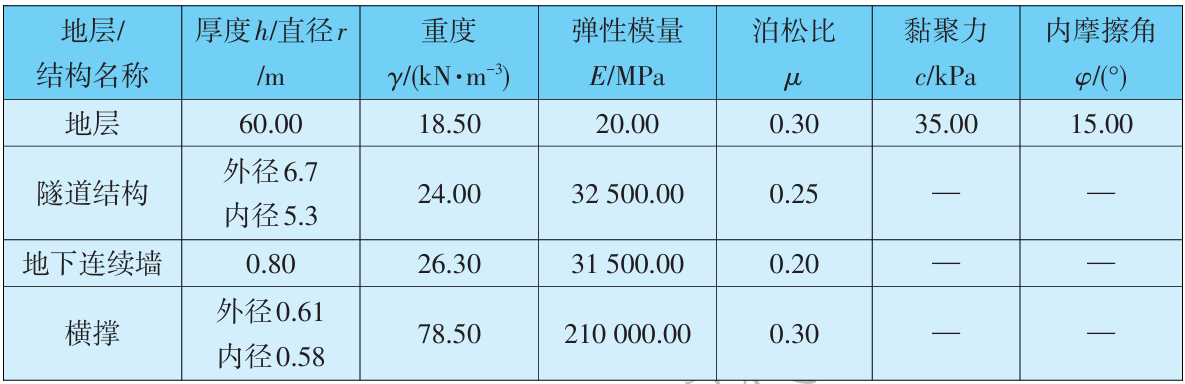
开挖基坑尺寸为20m(长)×20 m(宽)×30 m(深),采用地下连续墙与钢支撑相结合的支护方式,地铁2号线区间隧道埋深6m,水平方向上与基坑距离为12m。基坑与既有隧道结构的空间位置关系如图1所示,地层及结构的物理力学参数见表1。
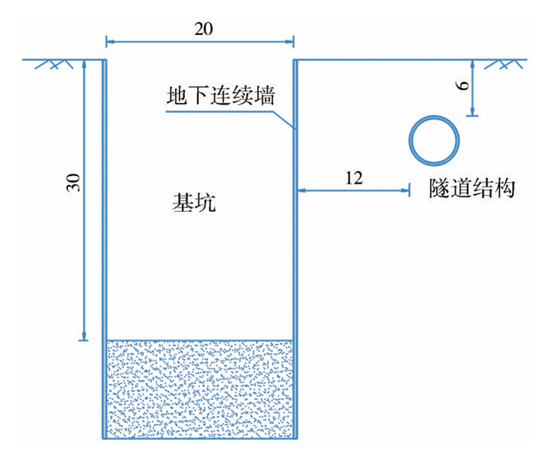
图1 基坑与隧道的位置关系(单位:m)
表1 地层及结构物理力学参数
3 基坑施工引起既有结构竖向位移分析
3.1 室内模型试验
3.1.1 相似比设计
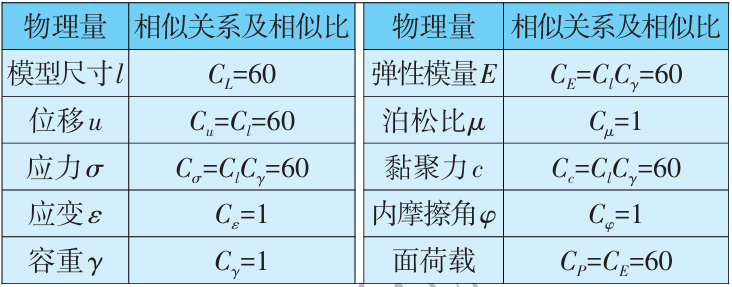
结合模型箱尺寸及试验仪器的相关参数,确定模型试验的几何相似比CL =60,容重相似比Cγ =1,以此作为基础相似比,通过相似关系推导出其他参数的相似比,见表2。
表2 模型相似关系
3.1.2 试验材料
(1)土样
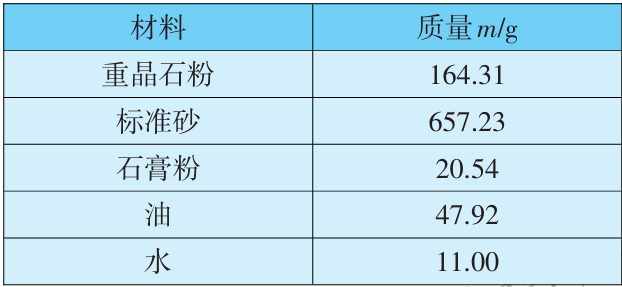
试验土样材料选用重晶石粉、标准砂、石膏粉、油和水,重度为18.5kN/m3,每种材料的质量见表3。通过直剪试验得到试验土样的黏聚力为0.213kPa,内摩擦角为30.09°。
表3 试验土样材料组成
(2)既有隧道结构及地下连续墙
隧道模型及地下连续墙采用有机玻璃(弹性模量为3.00 GPa)制作,隧道外径、地下连续墙宽度和高度通过几何相似比CL进行设计,隧道内径和地下连续墙厚度根据等效抗弯刚度公式(1)、(2)设计。
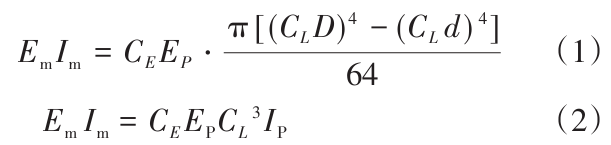
式中:Em、Im分别为原型材料的弹性模量及截面惯性矩;EP、IP分别为试验材料的弹性模量及截面惯性矩;CE、CL分别为弹性模量相似比和几何相似比;D、d分别为隧道的外径和内径。根据上式可计算得出模型隧道内径为160mm(外径为200mm),地下连续墙厚度为8mm。
(3)PVC管
施工现场的横撑结构常采用ϕ609钢管撑,其弹性模量为206GPa,试验采用PVC管(弹性模量为2.00 GPa)进行模拟,通过等效抗弯刚度公式(1)计算出其厚度为2mm,外径为15mm。PVC管端头采用橡胶片固定并与地下连续墙连接,如图2所示。

图2 采用PVC管模拟施工现场的横撑结构
3.1.3 试验过程
基坑开挖长度L=30cm,开挖宽度d=30cm,开挖深度H=50cm,既有隧道结构与地下连续墙的近接距离B=20cm,覆土埋深h=10cm,使用位移计监测既有结构拱顶及拱腰处的竖向位移。试验的模型箱为可视化结构,采用型钢和有机玻璃制成,尺寸为1.5 m(长)×0.8 m(宽)×1.2 m(高)。将隧道模型及地下连续墙放置在设计位置,填土至装满模型箱。设置沉降杆并安装位移计,待数据采集系统中数据变化较小时,即可开始试验。将基坑分为12层逐层开挖,每层的开挖厚度约为4.2cm,期间共安装3道横撑结构(分别位于地表以下-5cm、-20cm、-35cm),试验装置如图3所示。

图3 模型试验装置
3.2 三维数值模拟
采用FLAC 3D有限差分软件构建三维数值模型(图4),地层采用Mohr-Coulomb本构模型,隧道结构、地下连续墙及横撑采用弹性本构模型。基坑长20 m、宽20 m、深30m,地下连续墙由C35混凝土浇筑而成,既有隧道结构与地下连续墙的近接距离B= 12 m,覆土埋深h=6m。数值计算模型的施工过程共由两部分构成,其一为既有隧道区间及地下连续墙的施工,施工完成后进行位移清零,认为土体已完成固结沉降,仅存在应力场,将此状态作为基坑施工的初始状态;其二是基坑的施工,共分为12层逐层开挖,每层厚度为2.5m,期间共安装3道横撑结构(分别位于地表以下-3m、-12m、-21m)。
图4 三维数值模型
3.3 既有隧道结构竖向位移分析
将模型试验所得结果通过相应的相似关系(表2)转换为实际的竖向位移,其与数值模拟的结果均与实际工程相对应。既有隧道结构的竖向位移随施工步的变化曲线如图5所示。由图5可知,随着基坑开挖深度的增加,既有隧道结构的沉降值逐渐增大,在横撑2施作后,随着基坑开挖深度的持续增大,隧道的竖向位移快速增大,直到横撑3施作后,隧道的竖向位移开始缓慢增长。从整体来看,模型试验与数值模拟所展现的规律基本一致,均是随着基坑开挖深度的增大,隧道的沉降表现出“缓慢—快速—缓慢”增长的趋势,从而也证明了针对这一问题采用模型试验方法的可行性。
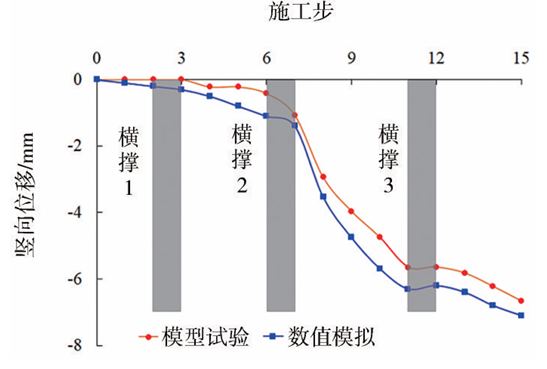
图5 既有隧道结构竖向位移随施工步的变化关系
3.4 地下连续墙所受土压力分布规律
通过改变基坑与既有隧道结构的近接距离、隧道埋深,在地下连续墙上每隔10mm布置1个土压力盒,监测施工过程中地下连续墙所受到的土压力,分析土压力分布规律,如图6所示。

图6 土压力盒布置示意
不同近接距离与不同隧道埋深下地下连续墙所受到的土压力与其埋置深度的分布规律如图7所示。可以发现,当隧道埋深不变时,随着近接距离的增加,地下连续墙所受到的土压力逐渐增加,这是因为既有隧道结构起到了“遮拦作用”,随着近接距离的增加,“遮拦作用”逐渐减弱,导致土压力变大;而随着地下连续墙埋置深度的增加,其所受到的土压力逐渐增加,直到超过基坑的开挖深度,土压力逐渐减小。由于既有隧道结构的存在,地下连续墙所受到的土压力均小于半无限土体下的土压力。
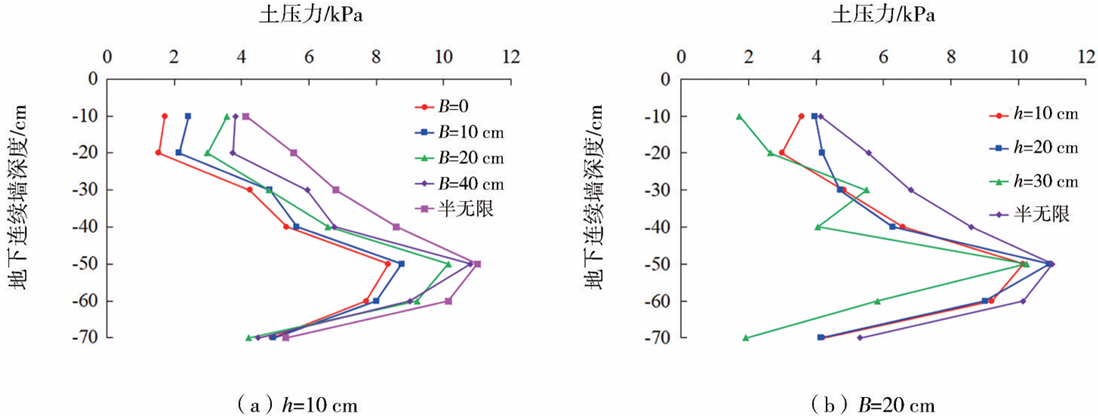
图7 地下连续墙所受土压力分布规律
3.5 地下连续墙水平位移分布规律
由于基坑开挖会导致土体向基坑内部发生挤出变形,导致地下连续墙产生水平位移。控制基坑与隧道的近接距离为12m,隧道埋深6m,提取数值模型中地下连续墙的水平变形分布曲线,如图8所示。可以发现,地下连续墙水平变形呈“两端小,中间大”的情况,水平变形随着基坑开挖深度的增大而逐渐增大,且墙体最大水平位移点随基坑开挖深度的增大而逐渐下移,开挖至基底时水平位移最大,最大值为29.5 mm。
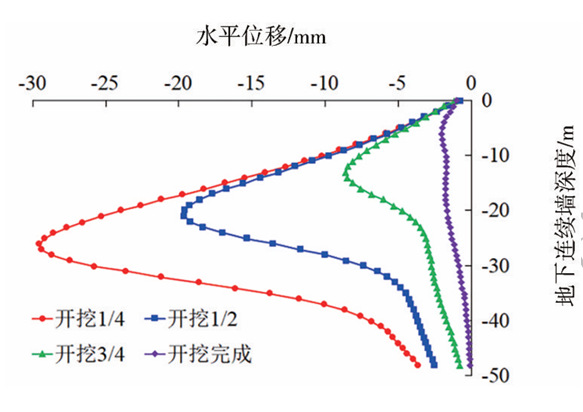
图8 地下连续墙水平位移分布规律
4 既有隧道结构变形模式
为研究既有隧道结构在基坑开挖影响下的变形模式,采用模型试验的方法,通过改变近接距离B及既有隧道结构埋深h,控制基坑开挖深度H=50cm不变,得到既有隧道结构的差异沉降,分析既有隧道结构的变形模式。
不同近接距离与埋深下既有隧道结构的差异沉降如图9所示。可以看出,当埋深一定时(6m),差异沉降随近接距离的增大逐渐减小,并逐渐趋近于0;当近接距离一定时(12m),差异沉降随埋深的增大而先增大后减小,并逐渐趋近于0。而且,当既有隧道结构与基坑近接距离B与其埋深h的比值(B/h)为一个定值时,既有结构的差异沉降也为一个定值。
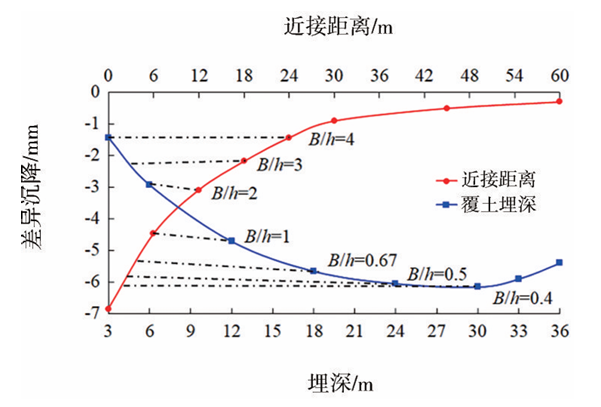
图9 不同近接距离与覆土埋深下的差异沉降
由于基坑开挖导致既有隧道结构一侧的土体会向基坑内发生挤出变形,既有隧道结构逐渐向扁平椭圆状的趋势发展,并随之产生不同的倾向。随着近接距离的增加,既有隧道结构一直呈现左倾的趋势,且左倾程度随近接距离的增大而逐渐减小。随着覆土埋深的增加,既有隧道结构一直呈现左倾的趋势,在开挖深度范围内,其左倾程度随埋深的增大先增加后减小。既有隧道结构倾向随近接距离与覆土埋深的变化示意图如图10所示。
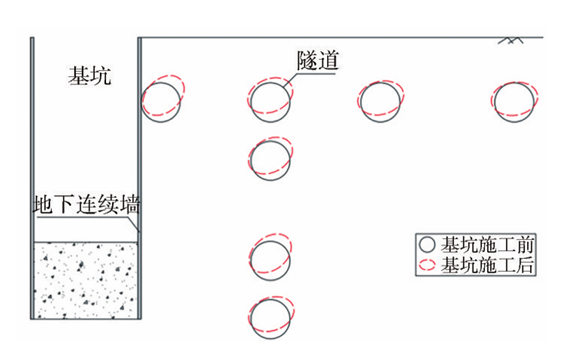
图10 既有隧道结构倾向示意
5 基坑施工影响分区
在基坑施工的影响分区方面,许多学者以不同的指标对影响分区做了划分,如地表沉降、既有隧道结构竖向变形、基坑的宽度和深度、围护结构水平变形、既有隧道结构水平距离及埋深、既有隧道结构的遮拦作用。然而,以既有隧道结构的差异沉降作为主要指标来界定影响分区却鲜有研究。差异沉降会导致隧道产生较大的不均匀变形和附加内力,尤其是盾构隧道,甚至会对管片、接头等部位造成严重危害。因此,有必要将差异沉降作为指标对影响分区进行划分。
5.1 施工影响分区
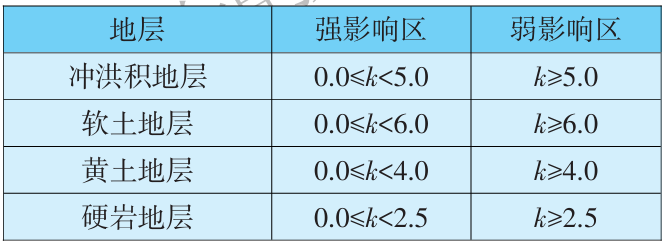
根据第4节的分析,当近接距离与埋深的比值一定时,既有隧道结构的差异沉降也为一个定值,所以,本小节定义一个近接系数k(k=B/h),通过改变k的取值(0.1、0.2、0.4、0.6、0.8、1.0、1.5、2.0、2.5、3.0,3.5,4.0,5.0,6.0,7.0,8.0),建立相关的数值模型,考虑上述两个影响因子(即B与h)进行综合分析。每一个近接系数建立3个模型(通过改变B与h的值,但k不变),取平均值确定此近接系数下既有隧道结构的差异沉降值,从而得出既有隧道结构的差异沉降与近接系数的关系,如图11所示。可以发现,当近接系数0.1≤k<5.0时,既有隧道结构的差异沉降变化较大,表明其受到基坑开挖的影响较大,左倾程度大;当近接系数k≥5.0时,既有隧道结构的差异沉降变化较小,直到无穷远处差异沉降为0。所以,以差异沉降减小与稳定的“拐点”作为划分标准,小于“拐点”一侧差异沉降较大,大于“拐点”一侧差异沉降较小。针对依托工程的地层情况,分别定义为强影响区(0.1≤k<5.0)与弱影响区(k≥5.0)。
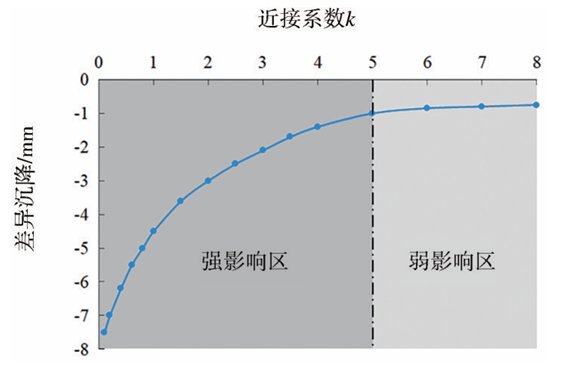
图11 既有隧道结构最大差异沉降与近接系数的关系
5.2 不同地层条件下的施工影响分区
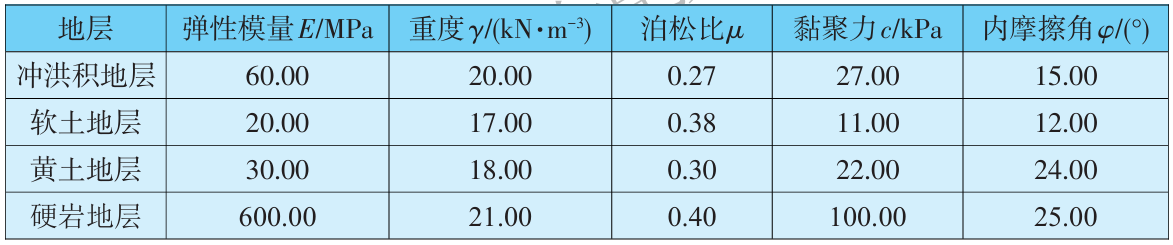
对于地层的选取,根据林攀[28]对全国已开通地铁的31个城市155个项目的地层情况的归纳和汇总,选取4种典型地层,分析不同地层条件对基坑施工影响分区的影响。4种典型地层的物理力学参数见表4。
表4 地层的物理力学参数
针对4种典型地层,根据近接系数的不同取值建立数值模型,计算得出不同工况中既有隧道结构差异沉降(图12),从而得出基坑施工影响分区范围(表5)。
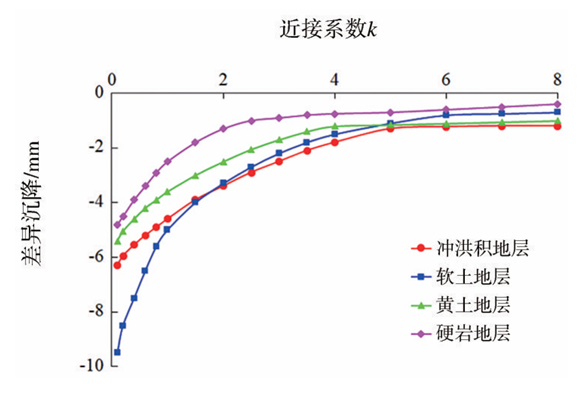
图12 不同地层基坑开挖引起既有隧道差异沉降
表5 不同地层中近接基坑影响分区范围
6 结 论
(1)既有隧道结构的差异沉降随基坑开挖深度的增加表现出“缓慢—快速—缓慢”的增长趋势,施工结束后的最大差异沉降为7.2mm,数值模拟和模型试验均显示出了一致的规律。
(2)由于基坑开挖过程中,土体向基坑内部发生挤出变形,地下连续墙产生水平位移,在开挖至基底时的水平位移最大,为-29.5mm。地下连续墙所受到的土压力随着基坑开挖深度逐渐增加,既有隧道结构存在“遮拦效应”,导致近接距离越大,土压力越大。
(3)既有隧道结构由于基坑施工产生的差异沉降随近接距离的增加逐渐减小,并逐渐趋近于0;而随着埋深的增加先增加后减小,临界点为基坑的开挖深度。
(4)基坑开挖过程中隧道结构逐渐向扁平椭圆状的趋势发展,既有结构左倾,随着近接距离的增加,基坑开挖对既有隧道结构的影响逐渐降低,既有结构左倾程度逐渐减小。
(5)当既有隧道结构与基坑近接距离B与其覆土埋深h的比值一定时,既有结构的差异沉降变化不大。将k=B/h定义为近接系数,根据近接系数k与差异沉降的关系,确定了在依托工程的地层情况下,0.1≤k<5.0 时为强影响区;k≥5.0时为弱影响区。并确定了4种典型地层下基坑开挖的危险程度,即软土地层>冲洪积地层>黄土地层>硬岩地层。
摘自《现代隧道技术》