0 引言
随着我国综合国力的提升,隧道工程建设取得了长足的进步。现有的长、大、难隧道普遍分布在我国西南地区,尤其是大变形灾害频繁出现,突出问题主要包括支护破坏、造价剧增、工期延长等。针对隧道大变形灾害,仅通过加强支护刚度的手段可能无法有效解决上述问题。而超前中导洞应力释放技术可使地应力得到部分释放,以此改善围岩中的应力场,正洞二次扩挖时,支护结构所承受的应力减小,保障支护结构的安全。
针对超前应力释放技术,尤其是中导洞应力释放技术,已有许多学者采用多种手段开展了相关研究,并取得了相关研究成果。赵勇等建立平面应变模型,根据理论计算引入应力折减系数考虑应力释放效应,并得出隧道变形的弹塑性解。夏才初等基于经典弹塑性力学理论,定义围岩应力释放比来反映应力释放的效果,分析了不同地应力、围岩弹性模量等指标对应力释放的效果的影响。祁和刚等提出了"高应力区段煤柱综合卸荷技术",采用小孔径爆破技术释放煤柱内的集聚载荷30%以上,取得了很好的变形控制效果。
高攀等为了控制木寨岭隧道的大变形问题,提出在变形较为严重、拆换比例高的地段采用超前大钻孔对地层高地应力进行释放,结果表明,超前钻孔对控制后期变形发展有利。刘建国对下导洞超前法在大断面山岭硬岩隧道中的应用效果进行了研究,结果表明,下导洞超前法能够达到排水释压的效果。李廷春依托兰渝铁路毛羽山隧道开展了现场试验,结果表明,采用超前导洞可有效降低正洞扩挖时的变形速率,对上中台阶影响尤为显著。郭小雄等依托某高地应力软岩隧道分析了超前中导洞合理尺寸及位置参数,提出了释放效果较好的参数组合。周宗青等依托石门垭隧道分析了包括全断面法、上下台阶法及导洞超前法的围岩变形控制效果,结果表明,导洞超前法施工引起的围岩变形最小。张梅等依托在木寨岭隧道和毛羽山隧道进行的超前导洞应力释放试验,提出采用超前导洞法可减小围岩变形量约30%~ 40%。由以上调研可知,目前对超前中导洞应力释放技术的研究主要集中于采用中导洞后的应力释放效果及中导洞大小、位置等合理参数的确定,对中导洞超前距离的研究较少。
中导洞超前距离的选取对应力释放效果有明显的影响,导洞超前距离较短可能使得应力释放率较小,甚至影响正常施工工序,导洞超前距离太长可能导致应力释放过度,导致围岩的弱化,无法达到减小隧道变形的目的。因此,中导洞合理超前距离的确定对施工具有重要意义。本文依托哈巴雪山隧道,对超前中导洞形状、尺寸及位置参数确定后,不同中导洞超前距离工况下隧道变形、支护结构受力及围岩塑性区进行研究,旨在确定合理的中导洞超前距离,研究结果可为日后类似工程提供参考与借鉴。
1 依托工程概况
滇藏铁路丽香段位于云南西北地区,全线新建20座隧道,总长约92.6 km,穿越地层岩性复杂、岩体软弱破碎、活动性断裂发育,具有高海拔、高地震烈度、高地应力的"三高"特征,隧道大变形问题极为突出。哈巴雪山隧道是丽香段大变形灾害最为严重的隧道之一,位于青藏高原东南缘横断山脉中段(见图1),隧道全长9.5 km,单线铁路隧道,最大埋深1 200 m,施工过程水平收敛达4 m以上,也是目前国内最严重的大变形隧道之一。
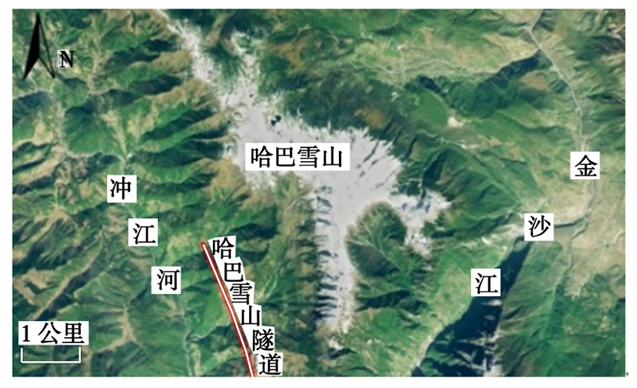
图1 哈巴雪山隧道位置
哈巴雪山隧道通过存在那田增正断层,主要岩性为片理化玄武岩、砂质板岩、板岩夹灰岩。该隧道地质纵断面图如图2所示,复合式衬砌参数如表1所示,正洞及中导洞设计断面如图3所示。
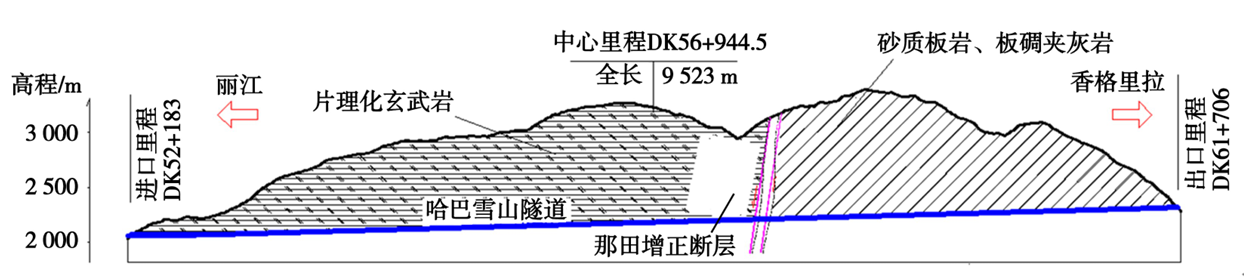
图2 地质纵断面
表1 正洞支护参数

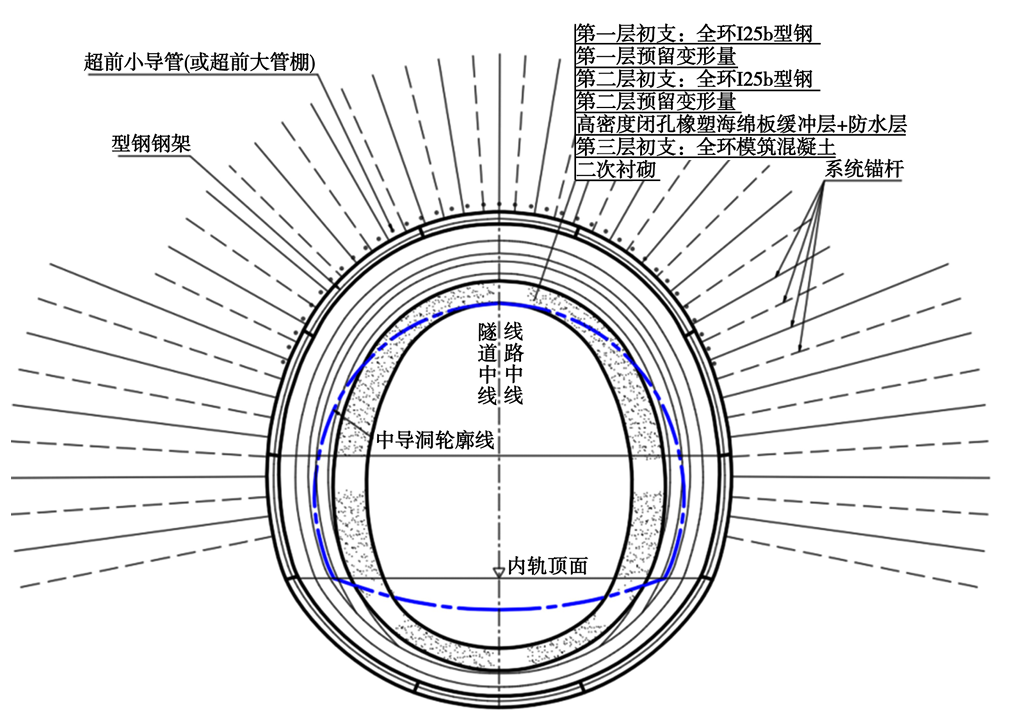
图3 哈巴雪山隧道断面图
哈巴雪山隧道由于埋深大、地应力高、地质构造复杂,在施工过程中隧道整体挤入严重,见图4,甚至出现了长达189 m的二次衬砌溃裂,见图5。

图4 隧道变形严重

图5 二次衬砌溃裂
2 数值模型与工况设计
2.1 数值模型建立
为了对中导洞合理超前距离进行研究,本文采用FLAC 3D有限元软件建立数值模型,模型尺寸及网格划分见图6。
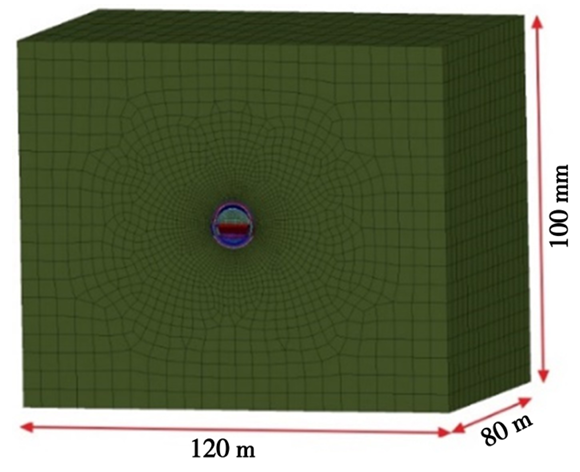
图6 隧道地层计算模型
本模型采用遍布节理模型(ubiquitous joint model),遍布节理模型是岩土工程中模拟含密集裂隙岩体的数值模型,假设节理均匀分布且方向固定,通过各向异性本构关系描述材料力学行为,结合了完整岩体与节理的强度准则。在模型计算过程中,岩体及结构面的参数见表2。初期支护物理力学参数见表3。
表2 岩体及结构面物理力学参数
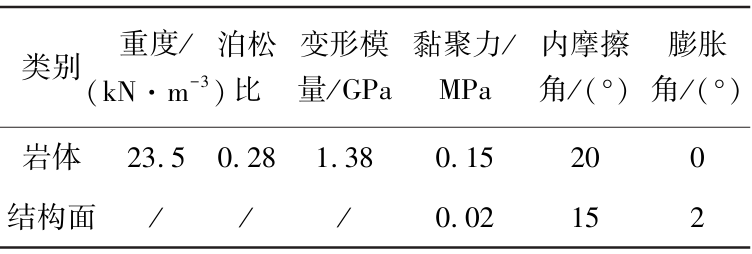
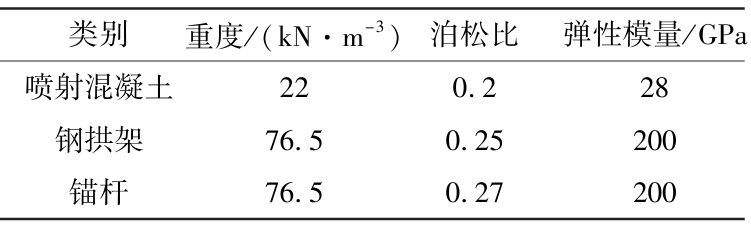
表3 支护结构参数
2.2 数值模型验证
为了确保计算模型的准确性,以数值模型中断面的变形与现场典型断面的变形量差异为指标校核计算模型。选用里程DK55+740正洞扩挖段为研究断面,可得数值模拟与现场监测结果对比如图7所示。
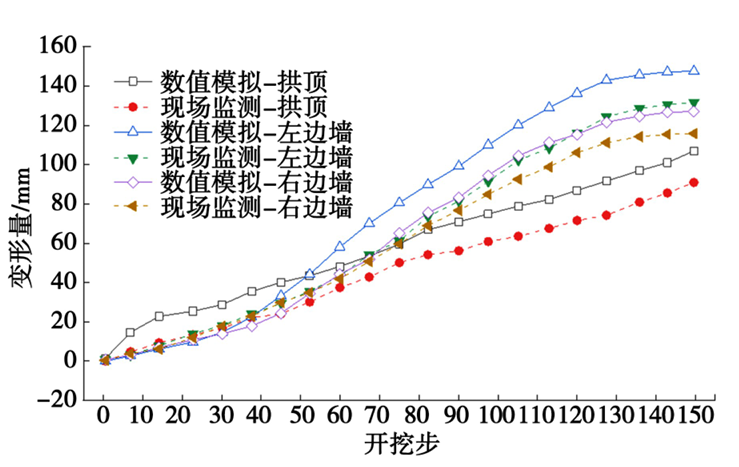
图7 数值模拟与现场实测数值对比
由图7可知,数值模拟结果与现场监测结果差异均较小。拱顶沉降、左右边墙水平收敛值差异分别为9.52%、10.76%、9.69%,可以认为该模型能够有效模拟实际施工,其计算结果在不同工程条件下均展现出较强的可靠性,可为多工况分析提供稳定支撑,确保预测结果与实际情况的一致性,从而为工程设计及安全评估提供可信依据。
2.3 工况设计
哈巴雪山隧道设计断面面积为115.98 m2,宽度为11.68 m,高度为12.49 m。设计中导洞断面面积为73.03 m2,宽度为10.27 m,高度为8.71 m,中导洞位于正洞中线,距正洞拱顶为182 cm。根据施工实际情况,选择中导洞超前距离L分别为10 m、15 m、20 m、25 m、30 m 5种工况,分别对应约1.0~3.0倍中导洞洞径。各工况模型示意图如图8所示。各工况参数如表4所示。
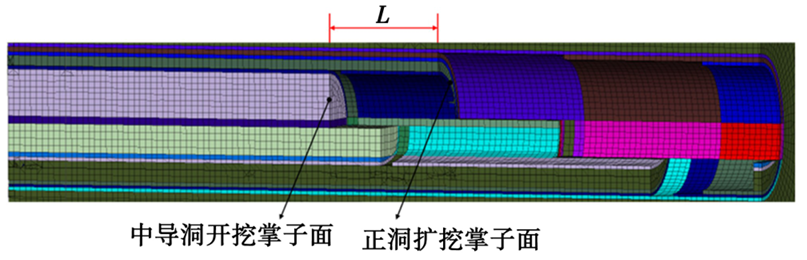
图8 中导洞超前距离L示意图
表4 不同工况超前距离数值

3 数值计算结果分析
3.1 拱顶沉降
为减小边界条件对计算结果的影响,研究选取Y轴方向30 m、40 m、50 m 3个典型截面作为监测对象,通过对各监测断面拱顶位移数据取平均,最终多工况对比分析结果见图9所示。
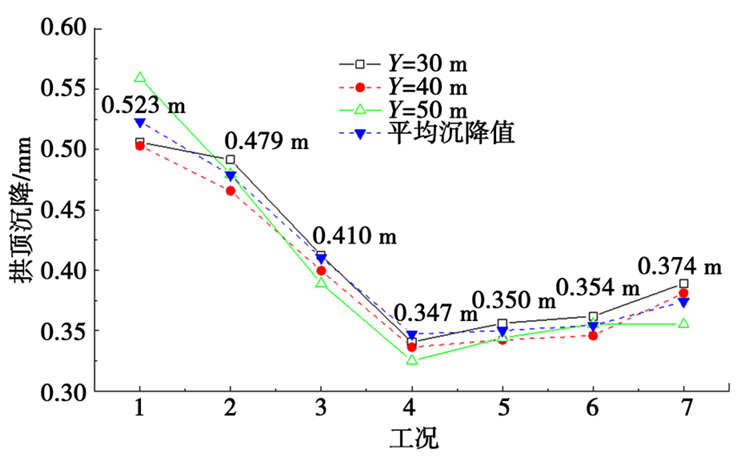
图9 不同工况下拱顶沉降值
根据图9数据对比可知,超前距离L与沉降量呈非线性关联:当L处于10~20 m区间时,沉降随距离增大呈递减趋势;当L超过20 m直至导洞贯通后,沉降量反向递增。数值分析表明,L= 20 m(约为2倍洞径)为最优参数,此时沉降值较无中导洞方案降低33.65%,验证了中导洞应力释放机制的有效性,较贯通后扩挖方案减少7.22%,证明合理控制超前距离可有效调控围岩应力重分布过程,实现沉降控制效果最大化。
3.2 水平收敛
在计算过程中监测Y=30 m、40 m、50 m 3个断面,提取各监测断面的水平收敛取平均值,得出不同工况下的水平收敛值如图10所示。根据图10对比分析,中导洞法显著降低了正洞上、下台阶的水平收敛变形量,结果表明,当超前距离L在10~20 m区间时,上、下台阶收敛量随L增大逐渐降低,当L超过20 m,上、下台阶收敛量出现逆向增长。因此,L=20 m(约2倍洞径)为最优参数,此时上、下台阶收敛量较无中导洞方案分别减少38.17%和38.84%,表明中导洞具有明确的围岩约束效应,且较贯通后扩挖方案也具有显著的围岩变形控制作用,上、下台阶收敛变形分别减小14.34%、20.72%,证实合理超前距离通过应力路径优化可有效减小围岩位移。
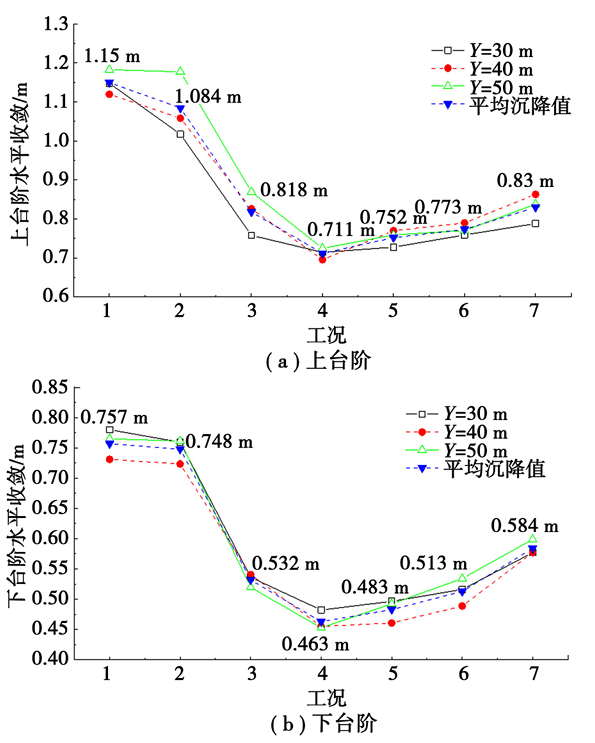
图10 不同工况下水平收敛值
由图9、图10可知,当采用中导洞时,隧道变形均随着中导洞超前距离L的增大呈现先减小再增大的趋势,这是由于当中导洞超前距离较小时,随着超前距离的增大,中导洞的应力释放效果增大,此时,正洞扩挖时的变形随着超前距离的增大而减小。当中导洞超前距离较大时,中导洞的应力释放效应使围岩劣化,正洞的变形减小幅度开始减小,甚至当中导洞超前距离大于合理值后,正洞的变形呈现增大的趋势。因此,中导洞超前距离若较短,达不到理想的应力释放效果,根据现场变形情况可知,支护变形速率在1—2月之内才会逐渐减缓,意味着围岩应力释放时间须在1—2月之内。相反,中导洞超前距离若较长,超前中导洞的初期支护参数无法满足围岩稳定要求,随着变形的增大,围岩失稳,支护结构产生了严重的破坏,围岩产生更大的松动范围,正洞二次扩挖时会承受更大范围的松动荷载。
3.3 初期支护应力
隧道开挖引发围岩连续变形时,支护体系与围岩形成协同变形机制,在此过程中支护结构受力呈现动态演化。当喷射混凝土内部拉/压应力超越材料承载阈值时,将产生张拉破裂或受压破坏。本工程采用C30喷射混凝土,其抗压与抗拉强度设计值fc、ft分别为14.3 MPa和1.43 MPa。为探究中导洞超前距离对支护结构受力的影响,本研究针对第三层初期支护开展多工况应力分析,数值模拟结果遵循拉应力为正、压应力为负的规定。
3.3.1 初期支护最大主应力
不同工况下Y=30 m、40 m、50 m断面初期支护各位置平均最大主应力曲线如图11所示。
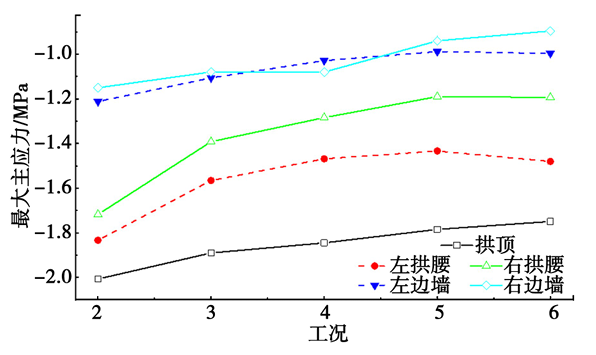
图11 隧道不同位置最大主应力
由图11可知,不同工况下各位置的初期支护最大主应力均为压应力,随着中导洞超前距离L的增大,各位置的最大主应力数值呈现逐渐减小的趋势,且压应力值均远远小于混凝土抗压强度设计值14.3 MPa。
3.3.2 初期支护最小主应力
不同工况下Y=30 m、40 m、50 m断面初支各位置平均最小主应力曲线如图12所示。
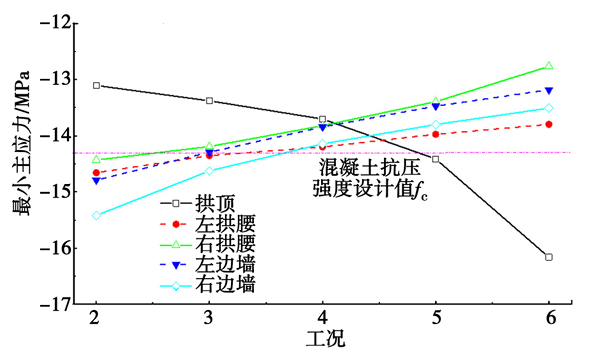
图12 不同工况各位置最小主应力曲线
由图12可知,各工况正洞初期支护均呈受压状态(最小主应力为负值)。拱顶位置的最小主应力数值随超前距离L增大不断增大,当L>20 m时突破C30混凝土抗压强度设计值(14.3 MPa),其机理在于超前距离扩展加剧了拱顶区域的应力集中效应。而隧道支护结构其他部位的最小主应力数值随L增大不断减小,在L>20 m时减小至至C30混凝土抗压强度设计值(14.3 MPa)以下,这与超前距离增大后应力释放效率提升导致的围岩荷载重分布密切相关。综合不同部位应力演化规律,确定L=20 m(约2倍洞径)为最优参数,该距离既控制拱顶应力集中程度,又通过充分应力释放优化整体支护受力状态。
3.4 围岩塑性区
本节由FLAC 3D求解并对比中导洞不同超前距离下的塑性区分布,为了定量描述围岩塑性区大小,采用CAD软件计算出围岩塑性区的面积,不同工况下的Y=40 m断面塑性区面积对比如图13所示。
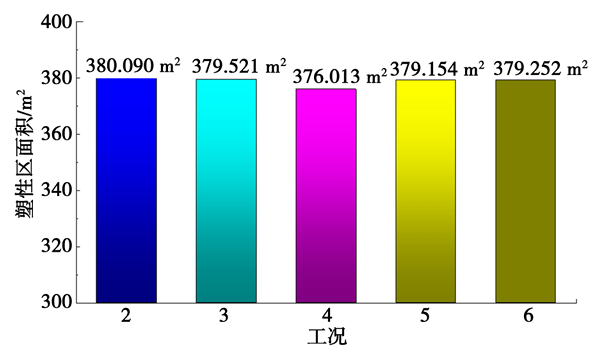
图13 不同工况下塑性区面积
由图13可知,不同中导洞超前距离下围岩的塑性区面积相差较小,在中导洞超前距离由10 m增大至20 m时,围岩塑性区面积由380.090 m2减小至376.013 m2,中导洞超前距离由20 m增大至30 m时,围岩塑性区面积由376.013 m2增大至379.252 m2,因此,超前距离为20 m时,围岩塑性区面积相对最小,为376.013 m2,因此,中导洞合理超前距离应为20 m。
4 应用效果
哈巴雪山隧道采用超前中导洞断面与正洞断面面积之比为0.62,导洞中线与正洞中线重合,导洞拱顶距正洞拱顶为2.0 m,超前距离为2倍导洞洞径。本节分析哈巴雪山隧道采用超前中导洞后隧道变形及支护受力,分析超前中导洞应用效果。
4. 1 隧道变形
哈巴雪山隧道采用中导洞前后各位置变形时程曲线如图14所示,其中,A代表采用中导洞之前,B 代表采用中导洞之后。 各位置最终变形量及变形减小率如表5所示。
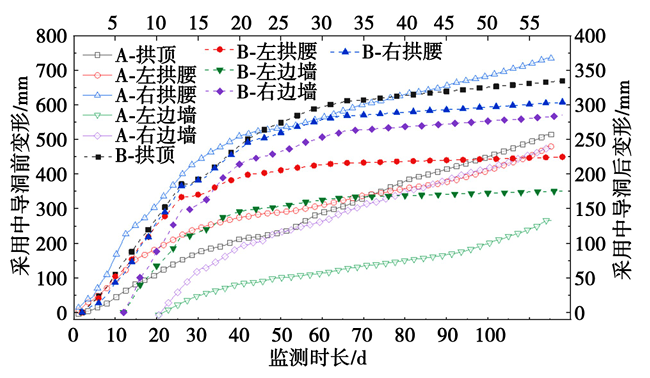
图14 隧道变形时程曲线
表5 各位置变形量(mm)

哈巴雪山隧道采用中导洞后,各位置变形量平均减小44.52%,变形控制效果显著,大大减小了支护结构破坏。
4. 2 衬砌结构受力
对采用中导洞前后正洞初期支护进行受力监测,采用中导洞前初期支护结构各位置围岩压力、钢筋应力及喷混应力时程曲线如图15、图16、图17 所示,采用中导洞后初期支护结构各位置围岩压力、钢筋应力及喷混应力时程曲线如图18、图19、图20 所示,采用中导洞前后初期支护结构各位置围岩压力、钢筋应力及喷混应力减小率统计如表6、表7、表8所示。
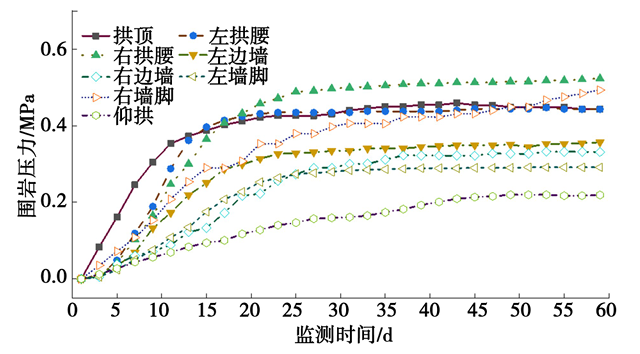
图15 围岩压力时程曲线
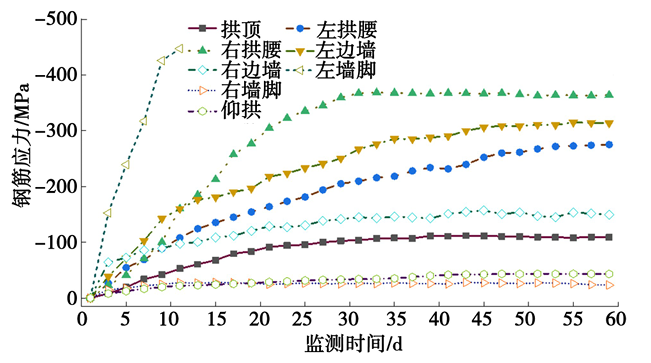
图16 钢筋应力时程曲线
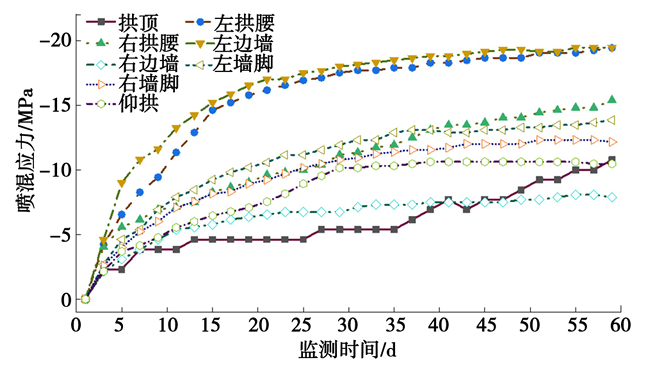
图17 喷混应力时程曲线
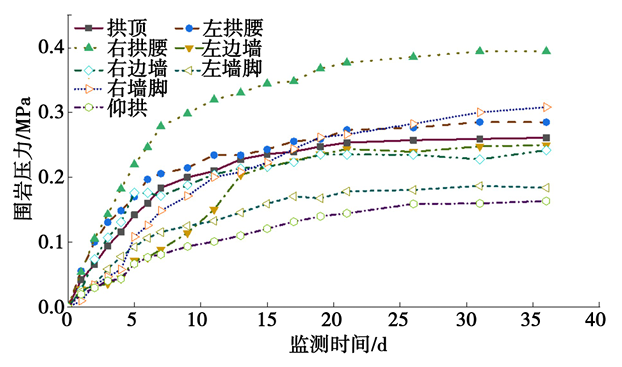
图18 围岩压力时程曲线
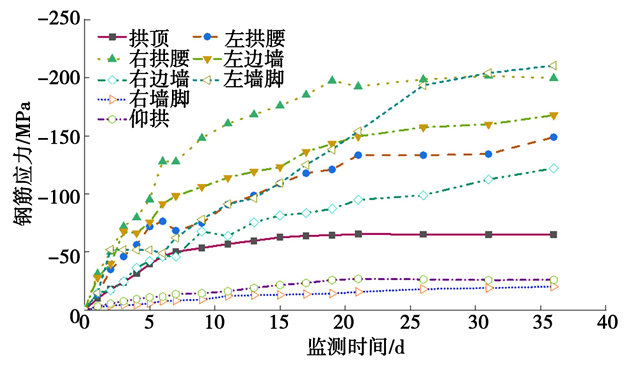
图19 钢筋应力时程曲线
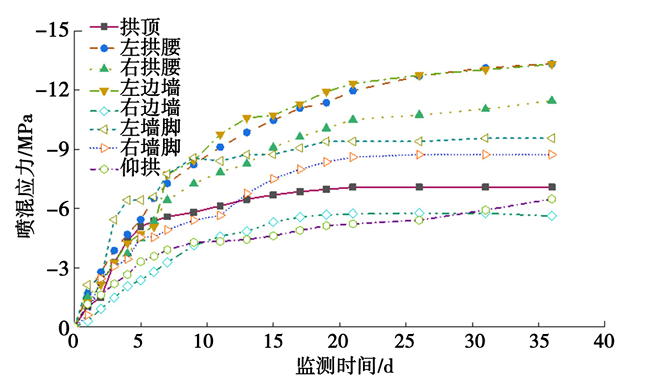
图20 喷混应力时程曲线
表6 围岩压力减小率(MPa)
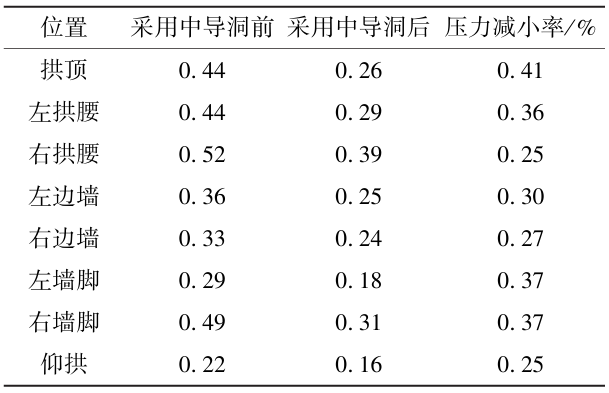
表7 钢筋应力减小率(MPa)
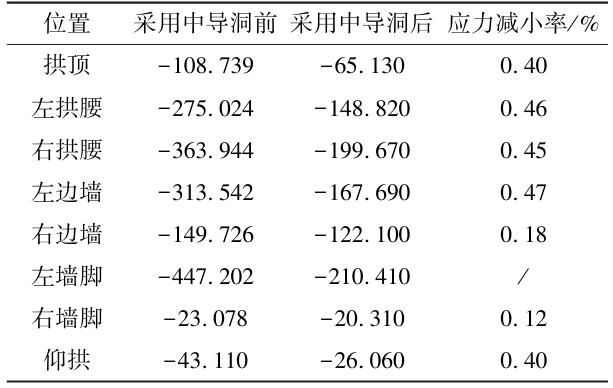
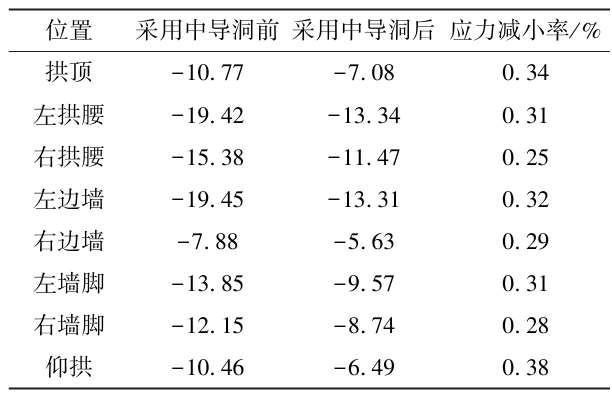
表8 喷混应力减小率(MPa)
由图15、图16、图17可知,哈巴雪山隧道采用中导洞前,初期支护结构受力较大,围岩压力最大位于右拱腰,达到0.52 MPa,超过支护结构承载能力(0.5 MPa);钢筋应力最大位于左墙脚,达到-447.20 MPa,超过钢筋抗压强度设计值;喷混应力最大位于左边墙,达到-19.45 MPa,超过C30混凝土抗压强度设计值。
由图18、图19、图20可知,哈巴雪山隧道采用中导洞后,初期支护结构受力较小。各位置围岩压力均小于0. 4 MPa,低于支护结构承载能力(0.5 MPa);钢筋均为受压状态,最大应力出现在左墙脚,最大值为-210.41 MPa,为钢筋抗压强度设计值的52.6%;各位置喷混应力均为负值(受压),最大喷混应力在左拱腰,为-13.34 MPa,未超过混凝土(C30)抗压强度设计值。
由表6、表7、表8可知,哈巴雪山隧道采用中导洞后围岩压力、钢筋应力及喷混应力均降低,围岩压力平均降低32%,钢筋应力平均降低35%(去除异常值),喷混应力平均降低31%。
对哈巴雪山隧道采用中导洞后变形及初期支护结构受力进行监测并分析,可知隧道各位置变形量平均减小44.52%,且初期支护围岩压力、钢筋应力及喷混应力平均降低32%、35%、31%,能够保证初期支护结构的安全,现场初期支护及二次衬砌结构施作效果如图21所示。

图21 现场支护结构
5 结论
(1)采用超前中导洞可减小隧道变形,随着中导洞超前距离的增大,隧道拱顶沉降及水平收敛均呈先减小后增大的趋势,中导洞合理超前距离应取20 m,约2倍中导洞洞径。
(2)选取中导洞合理超前距离时,相比未采用中导洞,隧道变形量平均可减小36.89%;相比中导洞贯通后再扩挖,隧道变形量平均可减小14.09%。
(3)当中导洞超前距离为2倍中导洞洞径时,初期支护最大、最小主应力均未超出混凝土强度设计值,且围岩塑性区面积相对较小。
(4)采用中导洞后,隧道变形量平均减小44.52%,且初期支护围岩压力、钢筋应力及喷混应力平均降低32%、35%、31%,受力较小,保证了支护结构安全。
摘自《地下空间与工程学报 》