0 引言
随着中国大中型城市人口密度逐年增长,政府对城市地下空间规划与建设的需求日渐多样化,地下隧道建设已逐渐成为城市基础建设中的重点研究领域。城市地下隧道施工方法主要有明挖法、钻爆法、新奥法、盾构法等[1] ,其中盾构法具备高效、安全、经济、绿色等优点,被广泛应用在城市地下隧道建设中。 但城区盾构施工对地层变形的控制要求严苛[2] ,现阶段因盾构掘进造成地表沉降超限而引发的安全问题层出不穷,因此合理地预测和控制盾构掘进导致的地表沉降问题尤为重要。
传统的经验与半经验法、解析解方法及数值模拟法[2-4] 通常基于大量假设,存在准确性和普适性较差
的问题,无法反映实际工况,且预测精度难以满足工程需求; 最重要的是,这些方法无法应对复杂地层环境
下盾构施工中随机性、不确定性和高度非线性的问题。近年来,机器学习已在图像识别、系统控制、市场分析等诸多领域取得了广泛应用。 机器学习方法因具备独特的信息处理能力,可从庞大的数据库中挖掘数据复杂的内在特征[5] ,同时具有强自适应性、高并行性、高容错率[2] 和处理非线性问题的优势,被广泛应用于盾构隧道智能建造领域中。 此外,现今我国盾构拥有量和掘进里程已居世界第一[6] ,且累计地铁运营里程高达7252. 73 km[7] ,这为机器学习方法在盾构掘进地表沉降预测领域中的应用提供了强大的数据支撑和保障。
本质上讲,基于“ 数据驱动” 的地表沉降预测是先将沉降影响因素和预测目标转换为数据形式,再建立
预测变量与目标间的数学联系;在“ 大数据” 背景下,机器学习具备数据特征自主识别能力和数据实时处理
能力,便于在盾构掘进全过程中实现智能化分析与决策。 此外, 机器学习模型的输入参数不受维度限制[8] ,可同时输入包括地层条件、掘进状态、施工条件等多种地表沉降影响因素,充分地考虑了众多因素间
的耦合作用。 构建地表沉降预测模型的关键点在于预测模型与输入参数的选取,输入参数的复杂度决定了模型的准确性与普适性。 如今机器学习已在盾构掘进地表沉降预测中取得了广泛应用。
传统的经验与半经验法、解析解方法及数值模拟法[2-4] 通常基于大量假设,存在准确性和普适性较差
的问题,无法反映实际工况,且预测精度难以满足工程需求; 最重要的是,这些方法无法应对复杂地层环境
下盾构施工中随机性、不确定性和高度非线性的问题。近年来,机器学习已在图像识别、系统控制、市场分析等诸多领域取得了广泛应用。 机器学习方法因具备独特的信息处理能力,可从庞大的数据库中挖掘数据复杂的内在特征[5] ,同时具有强自适应性、高并行性、高容错率[2] 和处理非线性问题的优势,被广泛应用于盾构隧道智能建造领域中。 此外,现今我国盾构拥有量和掘进里程已居世界第一[6] ,且累计地铁运营里程高达7252. 73 km[7] ,这为机器学习方法在盾构掘进地表沉降预测领域中的应用提供了强大的数据支撑和保障。
本文基于文献调研,总结盾构掘进地表沉降机器学习预测模型的最新研究进展,分别从数据库建立、输
入参数选取、预测目标和模型选取、模型超参数优化等方面阐述构建预测模型中的关键问题,讨论现阶段的研究进展与不足,并在已有研究的基础上进行分析和展望。
1 机器学习概述
机器学习是人工智能领域的分支,可从庞大的数据库中学习信息的“ 计算方法” 并模仿人类“ 经验决策” 的能力,使其在学习过程中产生与人类同等的“ 智慧” 模式。 基于这种新模式对事物未来的发展趋势进行预测以产生最优的决策效果。 机器学习按照学习方式可分为监督学习、半监督学习、无监督学习和强化学习 4 种类型,如图 1 所示。
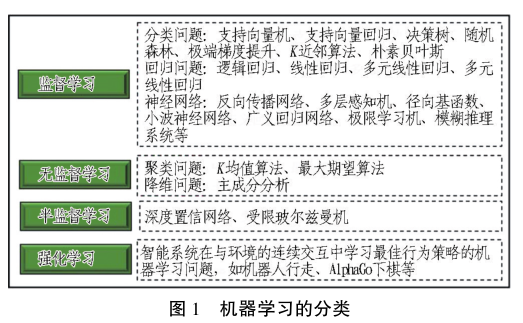
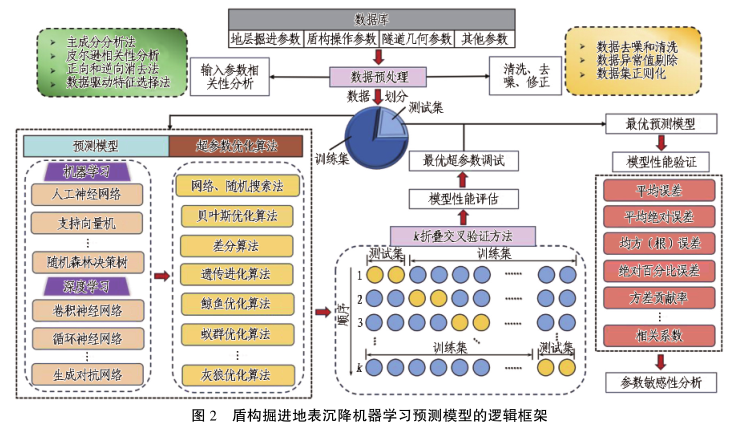
机器学习模型的建立主要包含数据采集、数据预处理、输入参数提取、模型训练、模型优化等 5 个步骤。其中数据采集主要依赖于现场传感器或特定的数据收集装置/系统,所采集的数据需经过清洗、去噪和修正等步骤处理后才能用于建模,然后根据所划分的数据集对模型进行训练和测试以评估模型的预测性能,最终依照评估结果通过适当的方法 ( 如调整模型超参数、增减数据集或变换输入特征) 进一步优化模型的预测性能。 基于上述分析,提出盾构掘进地表沉降机器学习预测模型的逻辑框架,见图 2。
2 数据库建立
数据预处理前需要对所采集的数据进行清洗,即把原始数据中有错误的、异常的数据转换成能输入到
模型中的数据形式。 其主要包括补全缺失数据、删除无效和重复数据、修正不准确数据以及统一数据输入格式等步骤。
2. 1 数据库预处理
2. 1. 1 异常值处理
数据清洗后仍可能存在偏离正常数据分布的离群值,这些异常值会严重影响数据样本区间的均值,进而
对模型的预测效果产生显著影响,因而有必要对数据库中的异常值进行处理。 现阶段数据异常值的处理方法主要有 3 种: 1) 裁剪异常值是一种直接有效的方法,保证数据集的可应用性; 2) 调整异常值的权重到
模型可接受的范围内,以降低和限制异常值的影响;3) 采用鲁棒性强的模型来实施预测,可降低异常值对
预测结果的影响( 例如: Mahmoodzadeh 等[13] 通过调整异常值的权重来控制模型的预测效果; Bo 等[14] 则将数据集中 3 倍标准差(3σ) 以外的异常数据用样本均值替代,而 Tang 等[15] 则删除了数据集中 3 倍标准差(3σ) 以外的异常数据) 。
2. 1. 2 数据标准化
当数据集中的特征数量较多时,会导致预测模型的精度降低,因此需要对数据集进行标准化处理,以提高模型的收敛速率,简化设计过程,进而增强预测模型的稳定性[16-17] 。 数据标准化处理的 2 种主要方法是z-score 标准化和最大最小标准化。 z-score 标准化通过公式 z = ( x-μ)/σ 来实现,其中 x 为原始数据,μ 为数据集均值,σ 为数据集标准差,z 为样本标准化后的值。 最大最小标准化通过公式 Snorm = ( S-Smin )/( Smax -Smin) 使数据压缩至[ - 1, 1] 或[ 0, 1] 区间,以改善数据的分布,其中 S 为实测数据,Smax 和 Smin 分别为 S 中的最大值和最小值,Snorm 为正则化后的数据。
2. 2 数据集划分
为验证模型准确性并确保模型具备良好的泛化能力,通常将数据集分成训练集、验证集和测试集。 其
中,训练集用于训练模型,通常在数据集中的占比最大;验证集主要用于评估模型的准确性并选择出模型的最优超参数; 测试集则用于评估模型在实际应用中的泛化能力和有效性。 目前大多研究常采用交叉验证的方法(cross-validation, CV)将数据集划分为不同的子集进行训练和验证,再通过测试集来评估模型的可应用性。
3 输入参数与性能评估
3. 1 参数分类与筛选
机器学习预测模型可高效、准确地探索地表沉降与其影响因素之间复杂多元的数学关系,从而实时准
确地预测地表沉降。 基于大量的文献调研可知: 影响地表沉降的因素主要有隧道几何参数、掘进地层参数、盾构操作参数和其他参数 4 类,如表 2 所示。
复杂多变的盾构掘进引起的地表沉降是多参数耦合作用下的结果[18-19] ,并不能由某一类别的参数单独
决定,且影响地表沉降的各类参数间通常无明显的关联性。 此外,随着盾构法的广泛应用,盾构掘进地表沉
降预测数据库不断更新和扩充。 从中选取复杂的输入参数会导致模型过拟合或不收敛,选取简易的输入参数又会降低模型的预测精度。 因此,如何有效地选取参数使预测模型具备高精度和强泛化能力是研究人员建模前需要首先考虑的问题。
现阶段采用多种参数分析方法来进行输入特征的筛选。 例如: 采用 Pearson 分析法[19-20] 评估多元的沉降影响因素与地表沉降间的相关性,排除与沉降预测无关的输入特征; 采用主成分分析方法( PCA) [21] 在保留所有输入特征的前提下,使用主成分作为输入参数从而降低了模型的输入维度; 采用正向消去法和逆向消去法[22] 分步保留和消除了对预测结果最有效和最无效的输入参数直至满足输入维度的阈值要求; 此外,Kim 等[23] 提出数据驱动特征选择法对输入特征进行评估和筛选后再用作预测模型的输入参数。
3. 2 参数的应用频次
图 3 统计了盾构掘进地表沉降预测数据库中各类参数的应用频次。 从图中可以看出: 在影响地表沉降
预测的各类参数中,盾构操作参数和掘进地层参数使用 的 频 次 较 高, 分 别 占 参 数 总 数 的 35. 43% 和40. 94%; 其次是隧道几何参数和其他参数,分别占参数总数的 15. 35%和 8. 27%。
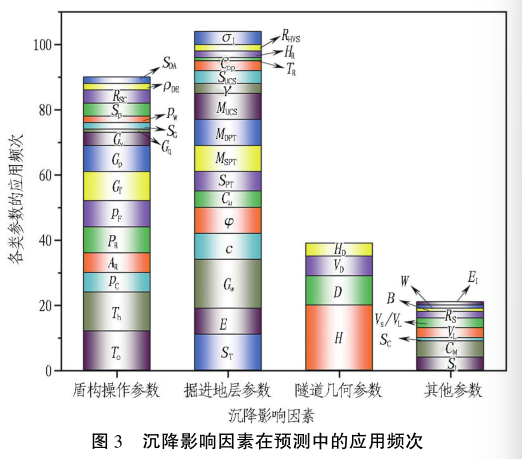
3. 2. 1 盾构操作参数
盾构操作参数在 4 类参数中的占比仅次于掘进地层参数,其中掌子面土压力(pF ) 、盾构推力( Th ) 、转矩( To ) 、舱室压力(pC ) 、盾构穿透率 ( PR ) 、推进速率(AR) 、注浆填充( Gf) 、注浆压力( Gp ) 、注浆体积( Gv ) 、注浆质量( Gq ) 等在沉降预测中的应用频次较高。 另外,盾构姿态( SG) 、盾构俯仰角( SP ) 、刀盘转速( RSC ) 、切割轮轮压(pW) 、进( 排) 泥量( SDA ) 、进( 排) 泥密度(ρDE ) 、 出渣量、 千斤顶速率等参数应用频次较低[2, 9, 12, 21, 24] 。 陈仁朋等[2] 指出从现场获取的注浆相关参数受施工条件的影响显著,往往难以直接用作模型的输入参数。
3. 2. 2 掘进地层参数
掘进地层参数通常难以确定和量化,这是因为不同类型地层的物理力学性质有所差异,而盾构掘进会
穿越不同类型的地层。 大多数研究通常对盾构所处地层进行简单划分,然后将所有地层性质的均值作为隧道所属地层性质的综合评价标准。 一些学者针对地层参数进行了优化设计,例如: Zhang 等[25] 认为地层变形与厚度近似成正比,便以厚度作为模型的输入参数避免了输入特征的复杂化; Chen 等[26] 考虑到地层深度和厚度对掘进进程的影响,引入厚度和深度修正因子对隧道覆土层的多种强度参数进行修正,以更为真实地表征地层的实际特性。
图 3 中指出应用频次较高的参数有: 地层类型( St) 和地下水( GW ) ,地层强度参数如弹性模量( E) 、
黏聚力( c) 、内摩擦角( φ) 、不排水抗剪强度( Cu ) 、标准贯入度( SPT) 、单轴抗压强度( SUC) ,修正地层强度参数[27] 如 修正单轴抗压强度( SMUC ) 、 修正标贯次数(MDPT) 、修正动探次数( MSPT ) 等应用的频次较高。 土体重度 ( γ) 、 围压 ( COP ) 、 现场应力 ( σi ) 、 岩体湿度(HR) 和温度( TR ) 、水平和竖向应力比( RHVS ) 等参数的应用频次较低。
3. 2. 3 隧道几何参数
在影响地表沉降的隧道几何参数中, 隧道埋深(H) 和直径( D) 是使用频率较高的参数; 当盾构隧道与既有隧道或地下管廊近距离施工时,则要考虑隧道间的水平距离( HD ) 和垂直距离( VD ) 的影响。 在单一盾构隧道掘进中,隧道直径的变化微小,通常被视为常数而不作为预测模型的输入参数[2] ; 但当涉及多条不同直径盾构隧道掘进或变截面盾构隧道掘进时,则必须考虑将直径作为输入参数来预测地表沉降。
3. 2. 4 其他参数
除掘进地层参数、盾构操作参数和隧道几何参数外,还有一些参数对地表沉降预测有着重要影响,如盾
构异常停机( St) [26-27] 、地面体积损失( VL) 和归一化体积损失( VS/VL) [28] ,隧道埋深较浅时临近建筑物的影响( 如建筑物宽度 B、质量 W、弯曲刚度 EI) [29] ,危险源(RS) ( 如地下溶洞) [30] ,盾构穿越复合地层或地层破裂区域[27] 的异常工况( SC) 和开挖方式( CM) 等。
3. 3 模型性能评估
模型性能评估是衡量模型预测效果的重要步骤。预测效果评估中常见的指标有: 均方误差( EMSE ) 、均
方根误差 ( ERMSE ) 、 平均绝对误差 ( EMAE ) 、 相关系数(R2) 等。 其中,EMSE 是计算测量值和预测值间平方误差的均值; ERMSE 是 EMSE 的平方根,二者的数值越小表示模型的预测效果越好; 是预测值与实测值间绝对误差的均值,越小表明预测的结果越准确; R2 用于度量模型拟合数据的程度,R2 越接近于 1 表示对数据的拟合效果越好。
4 地表沉降预测
盾构掘进导致的地表沉降按监测时间长短可分为短期沉降和长期沉降。 短期沉降通常发生在隧道开挖
几天或几周的时间内,有学者认为土体的不排水条件在短期沉降中占主导地位[3] ; 长期沉降则通常发生在隧道开挖几个月甚至几年时间内,主要与土体的蠕变、应力重分布、 土壤固结和孔隙水压消散等因素 有关[3] 。 在实际地表沉降预测研究中, 最大地表沉降( maximum surface settlement, MSS) 预测和时序地表沉降( time-series surface settlement, TSS) 预测是现阶段研究的重点内容。 最大地表沉降是指在盾构离开后每一环衬砌正上方地表沉降的稳定值; 时序地表沉降是指盾构掘进后每环衬砌上方地表沉降由小及大逐渐稳定的发展过程,能反映出地表沉降与复杂地层间的动态耦合关系,同时充分利用相邻环间的监测数据,实现地表沉降的实时动态预测[2] 。
4. 1 最大地表沉降预测
在同一案例中对比不同机器学习模型的预测效果,从而找到最优的预测模型( 本节括号中的数据均
为模型在测试集中的结果) 。 例如: 在最大地表沉降预测中,Chen 等[26] 认为 GRNN ( EMAE = 1. 66) 相比于BPNN ( EMAE = 2. 07) 和 RBF( EMAE = 2. 15) 有更高的预测精度; Chen 等[19] 进一步发现 GRNN ( EMAE = 1. 60)和 RF ( EMAE = 1. 85) , SVM ( EMAE = 1. 70) 相比于 ELM( EMAE = 2. 22) , MLR ( EMAE = 2. 31) 和 WNN ( EMAE =2. 18) , BPNN ( EMAE = 3. 35) 在沉降预测中表现出更高的预测精度, 但 SVM 的泛化能力较差不易使 用;Zhang 等[28] 基于同一数据库[19,26] 发现, RF ( EMAE =3. 03) 的沉降预测能力优 于 BPNN ( EMAE = 4. 20 ) ,GRNN ( EMAE = 4. 09) , SVM ( EMAE = 3. 74 ) 和 ELM( EMAE = 3. 99) 。 此外, Mahmoodzadeh 等[31] 认为深层网络模型 DNN ( EMAE = 2. 06) 和 LSTM ( EMAE = 2. 74)的沉降预测能力优于传统网络模型( KNN, GPR, DT,SVR 和 LR) 。 不同模型的预测误差和泰勒图解如图 4所示。
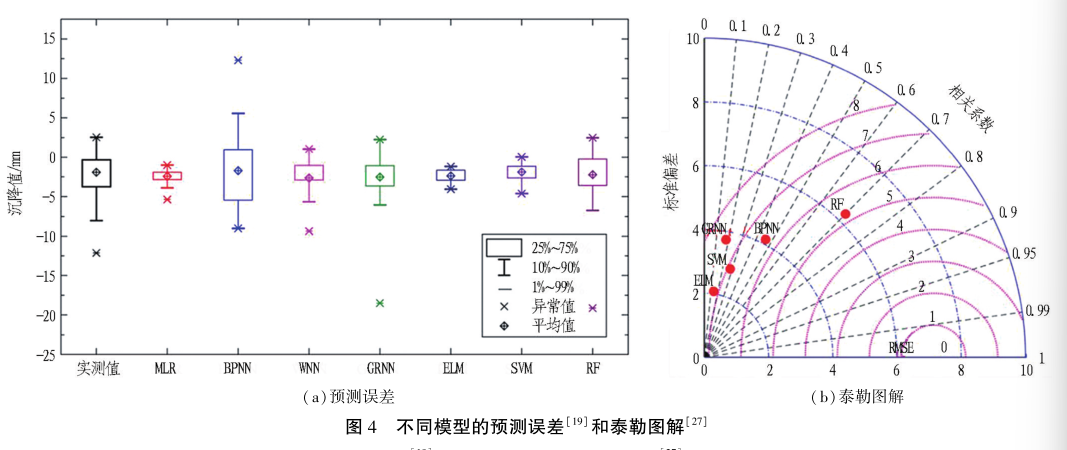
相关学者也对模型和参数的优化问题进行了探讨。 Hasanipanah 等[32] 将 PSO 与 ANN 相结合,大幅提高了模型的沉降预测能力,并设置了测试集验证了优化后模型性能的真实可靠性; Zhang 等[33] 使用 PSO 和GA 优化 SVM 的参数( c, g, γ) ,发现 PSO-SVM 相比于 GA-SVM 有更高的预测精度,均优于未经参数优化的 SVM 的预测精度,但这一研究并未设置测试集对优化后的模型进行性能验证; 有学者也指出使用GA[34-35] 、PSO[36-37] 算法优化模型参数可有效提高其沉降预测能力。 郝如江等[38]采用差分蚁群 优化( DEACO) 算法使 WNN 的沉降预测收敛速率和精度显著提高, 但 并 未 设 置 测 试 集 进 行 性 能 检验。 林荣安等[39] 还提出了一种基于粗糙集 -支持向量回归( RS -SVR) 的沉降预测模型,经过测试集的验证发现无论选用何种 SVR 核函数,RS-SVR 的沉降预测误差均小于SVR,例如: 当使用 RBF 作为核函数时, RS - SVR 和SVR 的预测误差分别为 5. 54% 和 13. 10%。 综上,尽管优化算法有助于提升原模型的预测效果,但仍需设置测试集对优化后模型的性能进行验证。
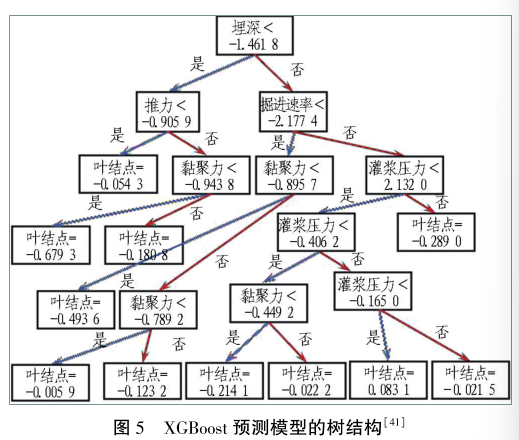
为清晰阐明沉降预测模型的内部运行机制。 Su等[40] 采用 XGBoost 模型( 见图 5) 避免了传统模型的
“ 黑箱性” 并详细展示了沉降的预测过程,研究结果表明: XGBoost ( ERMSE = 4. 005 ) 相 比 于 ANN ( ERMSE =6. 316) 和 SVM( ERMSE = 5. 356) 有更高的计算效率和沉降预测精度; ANFIS 赋予网络节点与权重相应的物理含义,具有计算量小、精度高、泛化能力强等特点,且在一定程度上避免了模型的“ 黑箱性” 。 李兴春等[41] 则使用 ANFIS 高效准确地实现了地表沉降预测。
适当减少预测模型中复杂的输入参数有利于提高模型的鲁棒性和预测准确性。 例如: 王祥等[42] 利用
RF 剔除了冗余的输入特征并降低了输入参数的维度,选取了最有效的特征作为 SVM 的输入参数,相比于不进行特征 选 择 SVM 的 预 测 准 确 性 大 幅 提 高; Ocak等[22] 通过 BF 和 FE 算法分步剔除了对沉降预测影响较小的输入参数,使经过特征筛选后的原模型( SVM和 ANN) 的 预 测 精 度 显 著 提 升; Bouayad 等[21] 通 过PCA 方法分析了所有的参数并选用主成分变量作为输入参数,在保留所有输入特征的同时降低了 ANFIS输入参数的维度,并实现了精准的地表沉降预测。
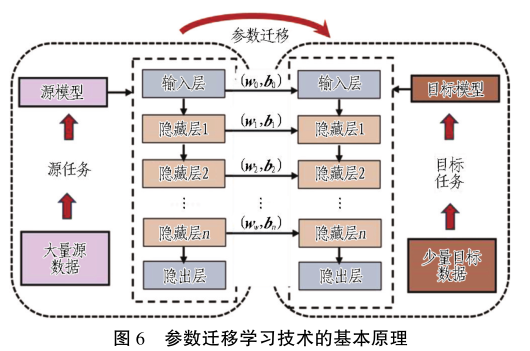
相关学者还探讨了数据库对模型沉降预测效果的影响。 例如: Fan 等[43] 指出 Dolsw 技术可用于提升训
练数据集的适用性和有效性,致使 Dolsw-SVM 的沉降预测相对误差低于 SVM; Mohammadi 等[44] 认为当数据集不足以支撑模型进行预测时,可采用数值分析法模拟现场工况来扩充数据集; 尽管 Zhou 等[45] 、陈仁朋等[2] 和 Zhang 等[28] 都认同 RF 具备较高的沉降预测精度,但 Mohammadi 等[44] 指出 RF 需要大量训练数据来确保其预测结果的准确可靠性。 值得一提的是,当存在高质量源数据且预测任务相关性较高时,迁移学习技术可有效解决数据集不充分的问题并保证预测的准确有效性,例如: Zhou 等[46] 采用参数迁移学习技术发现其预测精度相比 ANN 和 SVM 更高。 参数迁移学习的基本原理如图 6 所示。 图中 w 表示权重向量,b表示偏置向量。 为证实所提出的模型在不同案例中的适用性,对比了相同模型在不同数据集下的预测效果。例如: Tang 等[47] 使用数据集A构建了不同模型( DNN, RF, SVM, BPNN) ,并通过数据集 B 来验证这些模型的沉降预测性能,其中 RF 模型在 2 种数据集中均表现出优异的沉降预测效果。 此外,Zhang 等[30]还考虑了盾构掘进过程中邻近建筑物对地表沉降预测的影响。
综上,在最大地表沉降预测中,深层网络模型的预测效果优于传统 ANN; 使用 PSO、GA、BO、DE、ACO 等参数优化算法来提升模型的预测效果; 当模型的输入参数较冗杂时,建议采用 RF、FE、BE、PCA 等算法对输入参数进行筛选,以避免模型出现过拟合或无法收敛的问题; 此外,值得进一步考虑预测模型在不同数据集下的泛化能力,同时周边环境和建筑物对地表沉降的影响也值得进行深入研究。
4. 2 时序地表沉降预测
时序地表沉降预测主要关注的是盾构施工过程中某一环衬砌上方地表沉降的发展过程( 本节括号中的
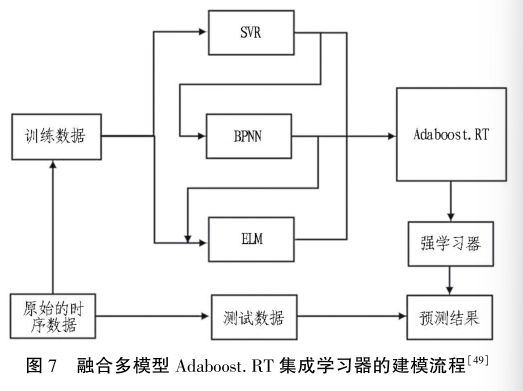
数据均为模型在测试集中的结果) 。 采用不同模型对地表沉降发展过程进 行 预 测 和 对 比 分 析。 例 如: Li等[48] 发现 LSTM( EMAE = 0. 79) 的沉降预测精度略高于GRU( EMAE = 0. 81 ) , 且二者的预测精 度均优于 RF( EMAE = 1. 02) ; 陈仁朋等[2] 则强调 RF 具有优异的沉降预测精度,同时具备优异的全局预测能力,可有效识别局部异常点位,适用于地表沉降发展过程的动态预测研究。 融合多模型 Adaboost. RT 集成学习器的建模流程如图 7 所示。 Yan 等[49] 在 Adaboost. RT 的基础上使用 BPNN、ELM 和 SVR 建立了集成学习器,结果表明: 集成学习器的预测效果显著优于单 一 模型( BPNN、ELM 和 SVR) 或 Adaboost 与单一模型所构建出的组合模型( Adaboost. RT - BPNN/ELM/SVR) 的预测效果。
针对模型和参数的优化,Kim 等[50] 使用 BO 方法优化了 SVR、RF、XGB、GBM 和 LGBM 5 种沉降预测模型的参数,并经测试集验证发现: 相比于不进行参数优化的原始模型,优化后模型的预测精度和收敛速度
均大 幅 提 高。 Cao 等[51] 将CEEMDAN 思想应用于LSTM 中, 并开发出一种预测精度高、 绝对误差小 的CEEMDAN-LSTM 沉降预测模型,对于不同案例中不同监测点,该模型在训练和测试集中均表现出了优异
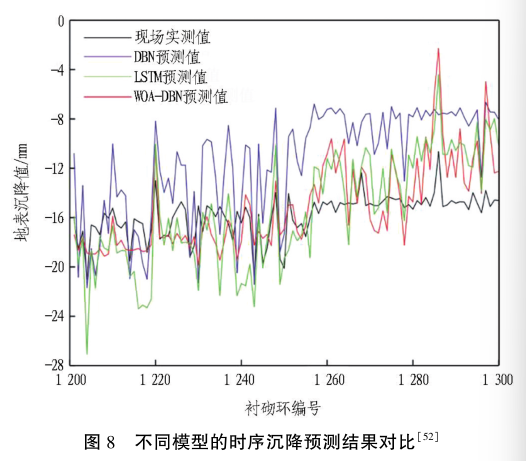
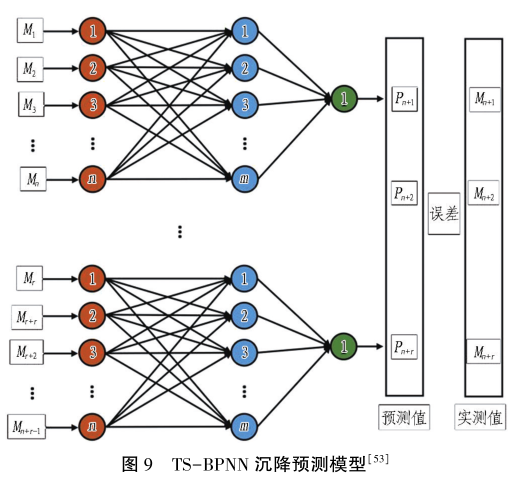
的沉降预测能力。 Ge 等[52] 对所提出的模型进行训练和测试 后 发 现: WOA - DBN ( ERMSE = 2. 875 ) 相比于DBN ( ERMSE = 5. 487) 和 LSTM( ERMSE = 3. 574) 表现出更高的预测准确性,如图 8 所示。 Ye 等[53] 使用实时监测和预测的地表沉降数据值作为 BPNN 的输入参数,提出基于时序的 TS-BPNN 模型( 见图 9,图中P和M 分别表示某一时刻模型的预测值和实测值) ,对不同沉降点在快速和缓慢沉降阶段的沉降进行预测,发现 TS-BPNN 均表现出了较高的预测精度。
为降低模型输入特征的维度,提高预测结果的可靠性,同时降低模型的运行成本,Ma 等[54] 选用最大信
息系数方法 ( MIC) 对 LSTM 模型的输入参数进行筛选,以提高计算效率和预测精度; Kim 等[23] 结合RF
与数据驱动特征选择法降低模型的输入维度。 相比于不进行特征筛选的模型而言,使用筛选后的参数所建立的模型具有更高的沉降预测精度。
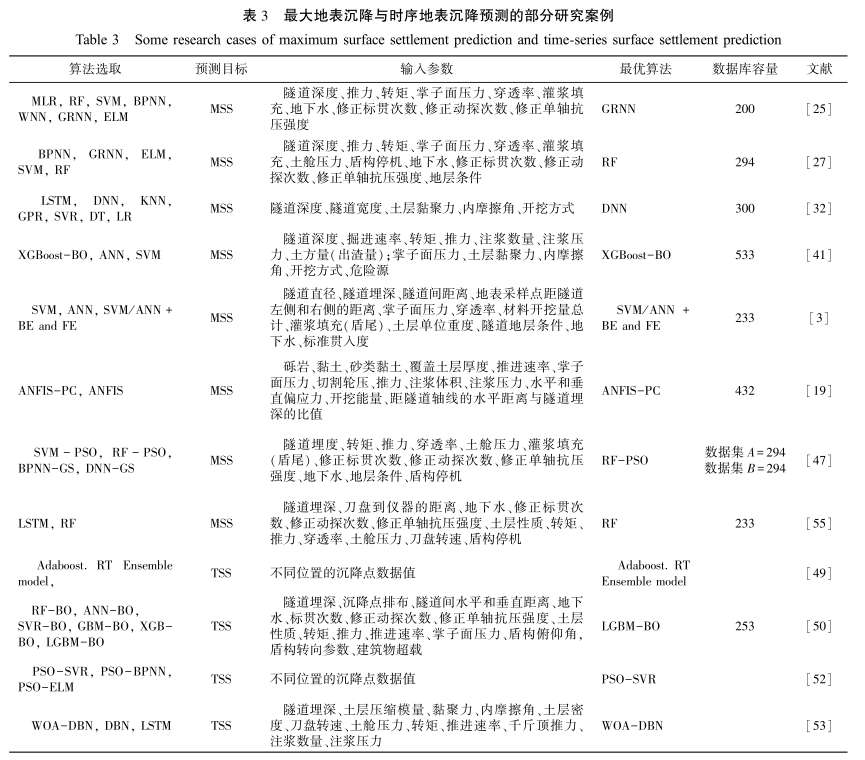
综上,传统的全连接神经网络并不适用于 TSS 预测,而 LSTM 可通过记忆单元捕捉和存储每一时间步
前后的信息,实现地表沉降发展过程的动态预测,并缓解 RNN 中常出现的梯度消失和爆炸的问题[2] ; RF 因具备较强的全局预测能力也常被用于 TSS 预测中。 为快速高效地优化模型的超参数并实现准确地预测,可采用 BO、PSO 和 WOA 等优化算法在测试集中对优化后模型的预测效果进行验证。 此外,最大信息系数和数据驱动特征选择法也为模型输入参数的筛选提供了新思路。 表 3 总结了MSS 和 TSS 预测局部分案例中的主要算法。
5 模型选取与超参数优化
5. 1 预测模型选取
机器学习具有独特的信息处理能力、强大的预测能力和灵活的网络架构,可处理变量间复杂的非线性
关系,在盾构掘进地表沉降预测中展现出了强大的应用潜力。 图 10 统计了近十年各类地表沉降机器学习
预测模型的应用频次。 结合第 4 节的分析可知: 人工神经网络、支持向量方法和基于树的方法等传统算法常被用于最大地表沉降的预测中。
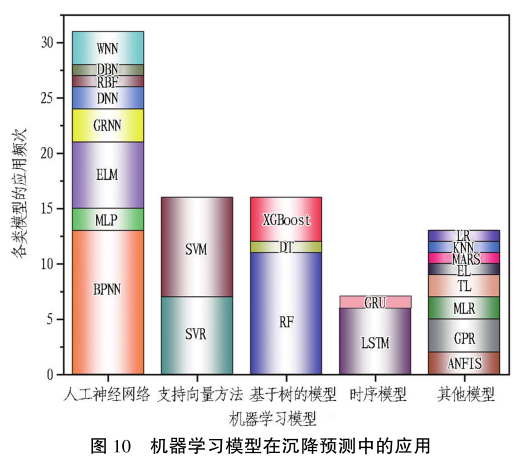
目前,人工神经网络依然是现阶段主流的沉降预测算法, 主要包括: BPNN、 MLP、 ELM、 GRNN、DNN、RBF、DBN、WNN 等多种类型。 尽管 ANN 存在固有的“ 黑箱性” 局限,无法清晰阐明变量与目标间的关系,但对于高维问题,ANN 相比于其他模型具有更强大的非线性拟合能力。 另外,支持向量方法( SVM 和 SVR)中的超参少且易于优化[19,22,33] ,该方法因其计算成本低常被用于模型性能的初步评估或预分析中,其通过核函数实现了数据从低维到高维空间的映射,并在高维空间中寻找超平面以求解预测问题,解决了数据维度对求 解 的 限 制。 此 外, 一 些 传 统 模 型 如 KNN[31] 、LR[31] 、MLR[44] 、MARS[56] 、GPR[31] 等也被用于最大地表沉降的预测中。 在收集长序列时间数据时会出现源数据质量不佳或数据集不充分等问题,可采用迁移学习的思想对源数据与目标数据间的特征进行学习,以参数迁移的方式在目标数据集中实现沉降预测。
在时序地表沉降预测研究中发现: 循环神经网络的变体 LSTM 和 GRU 因具有强大的信息连续动态捕
捉能力[2] ,可解决传统机器学习中“ 必须严格限制输入与输出间的对应关系” 这一固有局限[57] ,在沉降的动态预测中展现出强大的应用潜力; 此外,还发现通过集成学习思想建立的融合多模型的学习器在沉降发展过程预测中比单一模型具有更高的预测准确性和更强的鲁棒性,表现出优异的预测效果。
5. 2 模型的可解释性
“ 黑箱性” 问题是传统网络模型的典型特征,但基于树的模型可解决这一问题。 例如: XGBoost 可阐明
具体的沉降预测过程,且具有较高的计算效率和预测精度[40] ; ANFIS 可在一定程度上缓解模型的模糊性
问题,且其具备较强的泛化能力[20] 和较高的预测精度[2] 。 此外,集成多个 DT 的模型 RF 不仅可通过树结构清晰表达预测机制, 而且具有很强的全局搜索能力[2] ,同一案例中 RF 通常表现出比 ANN 和 SVM 更好的预测效果[19,26,28] 。
近年来已有研究逐步将物理方程引入到预测模型中以提高其可解释性。 例如: 张子龙等[57] 构建了地
表沉降与隧道开挖面的空间关联性,赋予了预测模型的物理含义; 潘秋景等[58] 提出的多域物理信息模型适用于不同地质和几何条件下盾构诱发地表沉降的预测; 张东明等[59] 将物理方程嵌入神经元中,构建了物理-数据双驱动的神经网络模型,实现了长距离隧道结构的纵向智能诊断; Zhang 等[60] 在机器学习模型中融合了土体的理论模型,发现嵌入物理信息后的预测模型对数据集的依赖性降低,表现出较强的泛化性;Zhang 等[61] 构建了一种能自动从测量数据中解答Terzaghi 固结理论的物理 - 信息双驱动网络模型;Zhang 等[62] 利用物理分层方法降低了预测模型对训练数据的需求,并提高其对土壤力学特性的预测精度。因此,后续研究应充分结合数理模型和数据驱动技术共同建立沉降预测模型。
5. 3 超参数优化算法
超参数是模型外部的配置值,须手动选取适当的值来使模型运行。 因此,模型的预测结果主要取决于最优的超参数组合。 试错法和微调法是常用的 2 种超参数调试方法。 其中,试错法的工作量巨大且难以得到较好的结果; 而微调法则是在具备一定参数选取经验的基础上探寻最优的超参数组合。
为实现模型超参数的精准调优,学者们提出了多种超参数智能优化算法,如 GSM、RSM、BO[40,50] 、元启发式算法等。 其中, 元启发式算法基于进化的GA[33,63] 、DE[64] 和基于种群智能优化的PSO[33,63] 、WOA[52,65] 、GWO[66-67] 、SSA[68-69] 、FA[70-71] 、ACO[38,63] ,已在模型超参数优化上取得了广泛应用。 表 4 总结了常见优化算法的优缺点。 然而,当数据库容量较高且模型超参数种类繁多时,采用智能优化算法调参往往会急剧增加计算成本[2] ,此时模型最优超参数的确定只能依赖于传统的试错法和微调法, 这一难题亟待解决。
6 结论与展望
6. 1 结论
本文对近十年间盾构掘进地表沉降机器学习预测中的最大地表沉降和时序地表沉降预测问题进行了分析和总结,认为机器学习方法促进了盾构隧道建设逐渐向高质量机械化和高效率智能化方向转变。 依靠机
器学习可深入挖掘数据的内在特征这一优势,针对不同的预测问题选用不同的机器学习方法实施精准的沉
降预测。 然而,当前研究仍存在以下问题亟待解决。
1) 数据的预处理和模型参数的选取依然是人为控制的,大量的人工注释和强烈的主观意识使数据库中的潜在特征被忽略。 如何使机器学习具备自主的数据处理和特征识别能力是未来研究中的关键问题。
2) 大多研究仅关注模型在同一案例中的预测效果,但相同模型在不同案例中因数据库和输入参数的差异通常表现出截然不同的预测结果,这导致模型难以在工程中推广应用。 建议充分挖掘和结合不同类型的数据,构建基于多源异构数据集的新模型,增强模型的泛化能力,以实现其在不同工程中的应用。
3) 使用机器学习进行地表沉降预测时常会出现过拟合现象,建议建模前对数据集进行预处理以去除噪声,当输入参数过于庞杂时,应对其进行筛选以降低维度; 当模型参数较多时,应使用参数优化算法来选择最优超参数; 当训练数据较少时,可采用迁移学习技术进行建模,从而在不同的预测场景中有效防止或减轻过拟合问题。
4) 现阶段多数地表沉降预测研究集中在最大地表沉降的预测上,针对时序地表沉降的预测研究较为
匮乏。 时序地表沉降预测中常用的 LSTM 模型通常仅将单变量的沉降值作为其输入参数,还应考虑众多变量在不同时间范围内的变化特征,开发出更为可靠的模型来实现沉降发展过程的预测。
6. 2 展望
在现有研究的基础上,未来机器学习预测的主要发展趋势如下:
1) 构建数理模型-数据双驱动的机器学习预测模型,通过融合或嵌入物理原理和数学方程赋予模型数理机制来提高其可解释性。
2) 通过对数据深度挖掘增强模型的泛化能力,这需要解决现阶段所采集的信息不同源和不兼容这一根
本问题。
3) 从算法的发展历程上看,深度学习方法相比机器学习能更精确地捕捉到数据内部的复杂特征; 从算法的分类上看,大多数现场数据是无标签的,需要通过大量的人工标注才能用于监督学习,因此无监督学习在未来有望成为主流的发展趋势。
4) 随着盾构掘进数据库的逐步扩张和智能算法能力的不断提升,有必要构建盾构隧道智能掘进平台,推动隧道工程建设朝向智能化和自动化方向前进。 机器学习在盾构掘进地表沉降预测研究中必有长足的发
展前景。